Сумою (об'єднанням) подій \(A\) і \(B\) називається подія, яка полягає в тому, що відбувається хоча б одна з даних подій. Суму подій \(A\) і \(B\) позначають (або ).
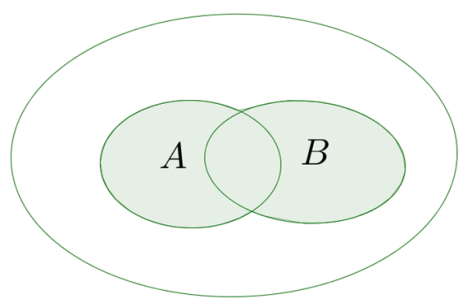
На малюнку за допомогою кіл Ейлера проілюстровано поняття суми подій \(A\) і \(B.\)
Велике коло уособлює всі елементарні події, які можуть відбутися в розгляненому випробуванні. Ліве коло уособлює подію \(A,\) праве — подію \(B,\) а зафарбована область — подію.
Добутком (перетином) подій \(A\) і \(B\) називається подія, яка полягає в тому, що відбуваються обидві ці події. Добуток подій \(A\) і \(B\) позначають \(AB\) (або ).
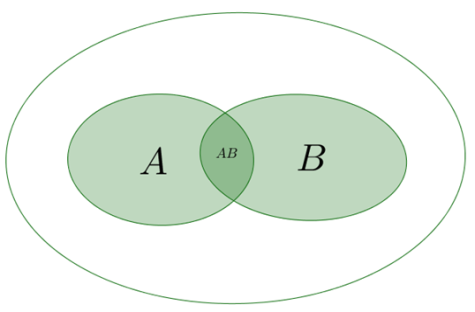
Малюнок ілюструє за допомогою кіл Ейлера добуток подій \(A\) і \(B.\)
Область, зафарбована темніше (спільна частина кіл \(A\) і \(B\)), ілюструє подію \(AB.\)
Події \(A\) і \(B\) називають рівними (рівносильними) й записують \(A=B,\) якщо подія \(A\) відбувається тоді й тільки тоді, коли відбувається подія \(B.\)
Наприклад, якщо у випробуванні з одним киданням грального кубика (подія \(A\)) випало число \(6,\) а подія \(B\) — випало найбільше з можливих чисел, то \(A=B.\)
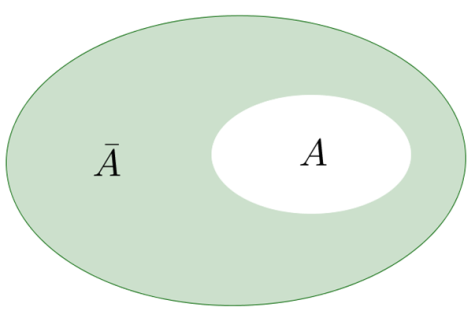
Подію називають протилежною події \(A,\) якщо подія відбувається тоді й тільки тоді, коли не відбувається подія \(A.\)
На малюнку проілюстровано взаємозв'язок подій \(A\) і на множині всіх елементарних наслідків випробування (подія зображена як зафарбована область).