1. Деякі символи математичної мови

Якщо до натуральних чисел приєднати число \(0\) та всі цілі від'ємні числа: \(-1, -2, -3, -4, ..., \) отримаємо множину цілих чисел. Цю множину зазвичай позначають буквою $\mathrm{\mathbb{Z}}$.

Якщо до множини цілих чисел приєднати всі звичайні дроби ($\frac{1}{3},\frac{51}{52},-\frac{8}{5},...$), отримаємо множину раціональних чисел. Цю множину зазвичай позначають буквою $\mathrm{\mathbb{Q}}$.

Множина $\mathrm{\mathbb{Q}}$ раціональних чисел — це множина, що складається з чисел вигляду $\frac{m}{n};-\frac{m}{n}$ (де \(m,n\) — натуральні числа) та число \(0\).

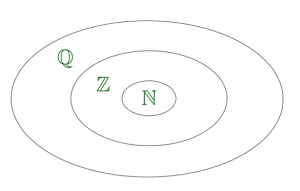
Зрозуміло, що $\mathrm{\mathbb{N}}$ — частина множини $\mathrm{\mathbb{Z}}$, а  $\mathrm{\mathbb{Z}}$ — частина множини $\mathrm{\mathbb{Q}}$. Для опису цієї ситуації в математиці також є спеціальне позначення: $\mathrm{\mathbb{N}}\subset \mathrm{\mathbb{Z}};\mathrm{\mathbb{Z}}\subset \mathrm{\mathbb{Q}}$.

Математичний символ $\subset$ називається знаком включення (однієї множини до іншої).

Запис $x\in X$ означає, що \(x\) — один із елементів множини \(X\).

Запис $A\subset B$ означає, що множина \(A\) є частиною множини \(B\). Математики частіше кажуть так: \(A\) — підмножина множини \(B\).

Для запису про те, що елемент \(x\) не належить множині \(X\) або що множина \(A\) не є частиною (підмножиною) множини \(B\), використовують ті ж самі символи, але перекреслені скісною рискою: $x\notin X,A\not\subset B$.

Наведемо кілька прикладів використання введених математичних символів для скорочення запису правильних математичних тверджень — їх називають також істинними виразами.

Будь-яке раціональне число можна записати у вигляді кінцевого десяткового дробу або у вигляді нескінченного десяткового періодичного дробу:

$\begin{array}{l}\frac{7}{22}=\mathrm{0,3181818}...=\mathrm{0,3}(18)\\ 4=\mathrm{4,000}...=\mathrm{4,}(0)\\ \mathrm{7,3777}=\mathrm{7,37770000}...=\mathrm{7,3777}(0)\end{array}$

Правильно й протилежне: будь-який нескінченний десятковий періодичний дріб можна подати у вигляді звичайного дробу. Це означає, що будь-який нескінченний десятковий періодичний дріб є раціональним числом.

Покажемо на прикладі, як нескінченний десятковий періодичний дріб перетворюють на звичайний дріб.