Функція квадратного кореня, її властивості та графік

Для побудови графіка функції

y = \sqrt{x}

надамо незалежній змінній \(x\) декілька конкретних значень (невід'ємних, оскільки якщо \(x < 0\), то вираз

\sqrt{x}

не має сенсу), а також обчислимо відповідні значення залежної змінної \(y\).

Звісно, ми будемо надавати \(x\) такі значення, для яких точне значення квадратного кореня є відомим.

Отже:

якщо \(x=0\), то

y = \sqrt{0} = 0

;

якщо \(x=1\), то

y = \sqrt{1} = 1

;

якщо \(x=4\), то

y = \sqrt{4} = 2

;

якщо \(x=6,25\), то

y = \sqrt{6.25} = 2.5

;

якщо \(x=9\), то

y = \sqrt{9} = 3

У такий спосіб ми склали таблицю значень функції:

\(x\)	\(0\)	\(1\)	\(4\)	\(6.25\)	\(9\)
\(y\)	\(0\)	\(1\)	\(2\)	\(2.5\)	\(3\)

Побудуємо знайдені точки \((0; 0), (1;1), (4; 2), (6.25; 2.5), (9;3)\) на координатній площині.

Вони намічаються певною лінією, накреслимо її.

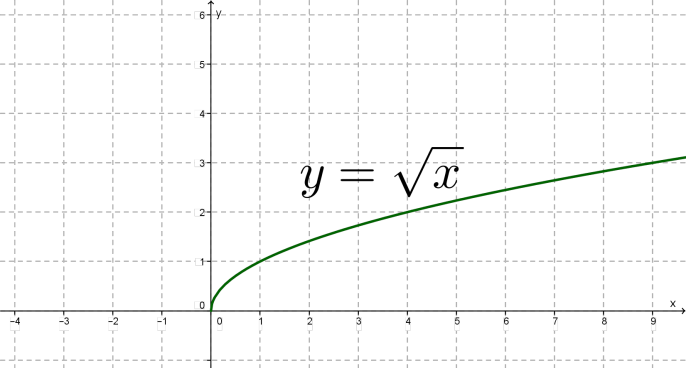
Ми отримали графік функції

y = \sqrt{x}

Зверни увагу!

Графік дотикається осі \(y\) в точці \((0; 0)\)

Зауважимо, що, маючи шаблон параболи

y = x^{2}

, з його допомогою можна легко побудувати графік функції

y = \sqrt{x}

, адже це — вітка тієї ж параболи, тільки орієнтована не вгору, а вправо.

Властивості функції

y = \sqrt{x}

Описуючи властивості цієї функції, ми, як завжди, будемо спиратися на її геометричну модель — вітку параболи.

1. Область визначення функції — промінь

[0; + \infty)

2. \(y = 0\), якщо \(x = 0\); \(y >\)0, якщо \(x > 0\)

3. Функція зростає на промені

[0; + \infty)

4. Функція обмежена знизу та необмежена зверху

y_{найм} = 0 при x = 0; y_{найб} не існує

6. Функція неперервна на промені

[0; + \infty)

Знайшли помилку?

1. Функція квадратного кореня, її властивості та графік