Властивості функцій , якщо \(k > 0\)
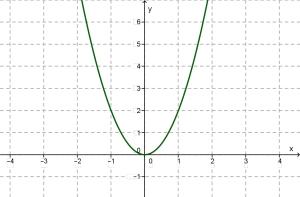
1. Оскільки для будь-якого значення \(x\) за формулою можна обчислити відповідне значення \(y\), то функція визначена в будь-якій точці \(x\) (за будь-якого значення аргументу \(x\)).
Коротше це записують так: область визначення функції є , тобто вся координатна пряма.
2. \(y = 0\), якщо \(x = 0\); \(у > 0\), якщо . Це видно і з графіку функції (він увесь розташований вище від осі \(x\)). Але це можна обґрунтувати й без допомоги графіка: якщо , тоді як добуток двох додатних чисел \(k\) та .
3. — неперервна функція.
4. (досягається, якщо \(х = 0\)); не існує.
5. Функція зростає, якщо та спадає, якщо .
У \(7\)-му класі процес перерахування властивостей функції ми називали читанням графіка.
Процес читання графіка ставатиме все більш насиченим і цікавим, адже ми будемо вивчати нові властивості функцій.
П'ять перерахованих вище властивостей ми обговорювали в \(7\)-му класі для вивчених тоді функцій. Додамо одну нову властивість.
Зверни увагу!
Функцію \(у = f(x)\) називають обмеженою знизу, якщо всі значення функції є більшими від певного числа. Геометрично це означає, що графік функції розташований вище від певної прямої, паралельної осі \(x\).
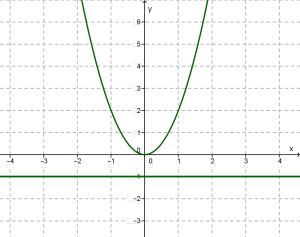
Отже, \((k > 0)\) — обмежена знизу функція.
Поряд із функціями, обмеженими знизу, розглядаються і функції, обмежені зверху.
Функцію \(у = f(x)\) називають обмеженою зверху, якщо всі значення функції є меншими від певного числа. Геометрично це означає, що графік функції розташований нижче від певної прямої, паралельної осі \(x\).
Отже, ми отримали ще одну властивість. Додамо її до тих п'яти, які вказані вище.
6. Функція \((k > 0)\) обмежена знизу та необмежена зверху.
7. Область значень функції \((k>0)\) — промінь .
8. Функція опукла вниз.
Властивості функції , якщо \(k < 0\)
Описуючи властивості цієї функції, ми спираємося на її геометричну модель — параболу.
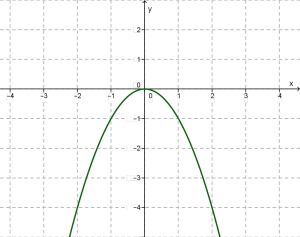
1.Область визначення функції .
2. \(у = 0\), якщо \(х = 0\); \(у < 0\), якщо .
З. — неперервна функція.
4. (досягається, якщо \(х = 0)\), не існує.
5. Функція зростає, якщо , убуває, якщо .
6. Функція обмежена зверху і необмежена знизу.
7. Область значень функції \((k<0)\) — промінь .
Використаний вище порядок кроків під час перерахування властивостей функції не є законом.
Поки що він склався хронологічно саме таким.
Поки що він склався хронологічно саме таким.
