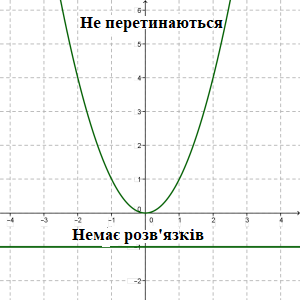
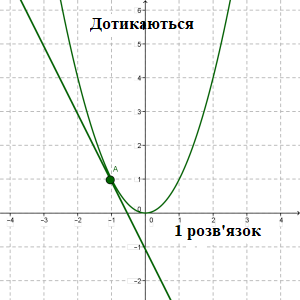
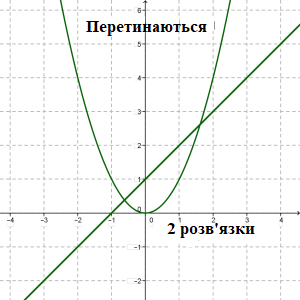
Підсумуємо наші знання про графіки функцій.
Ми з вами навчилися будувати графіки наступних функцій:
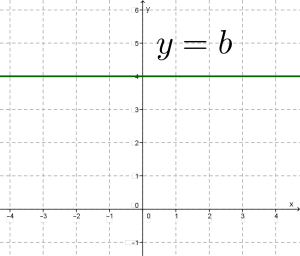
- \(y =b\) — пряму, паралельну осі \(x\);
- \(y = kx\) — пряму, що проходить через початок координат;
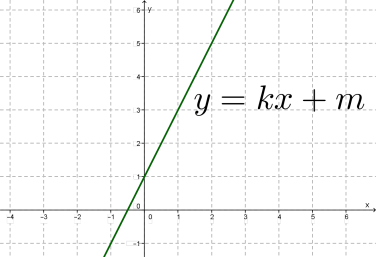
- \(y = kx + m\) — пряму;
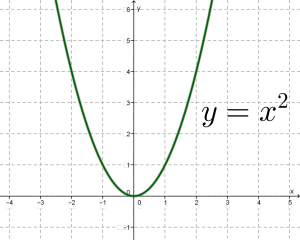
- — параболу.
Знання цих графіків дозволить нам у разі необхідності замінити аналітичну модель на геометричну (графічну). Наприклад, замість моделі (яка є рівністю з двома змінними \(x\) і \(y\)) розглядати параболу в координатній площині.
Іноді це корисно для розв'язання рівнянь. Як це робиться, проілюструємо на декількох прикладах.
Приклад:
Розв'яжи рівняння:
Розглянемо дві функції: та \(y = x + 2\), побудуємо їх графіки та знайдемо точки перетину графіків.
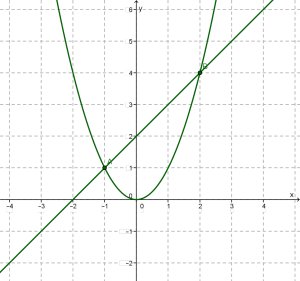
Парабола і пряма \(y = x + 2\) перетинаються в точках \(A (- 1; 1)\) і \(B (2; 4)\).
Як же знайти корені рівняння , тобто ті значення \(x\), за яких вирази і \(x + 2\) набувають однакових числових значень? Дуже просто, ці значення вже знайдені: . Це абсциси точок \(A\) і \(B\), в яких перетинаються побудовані графіки.
Алгоритм графічного розв'язання рівнянь
2. Побудова в одній системі координат графіків функцій.
3. Знаходження точок перетину графіків функцій.
4. З'ясування в них значень абсцис.