Функція та її графік
Розглянемо функцію та побудуємо графік її функції.
Надамо незалежній змінній \(x\) декілька конкретних значень та обчислимо відповідні значення залежної змінної \(y\) (за формулою ):
Ми склали таблицю:
| \(x\) | \(0\) | \(1\) | \(2\) | \(3\) | \(-1\) | \(-2\) | \(-3\) |
| \(y\) | \(0\) | \(1\) | \(4\) | \(9\) | \(1\) | \(4\) | \(9\) |
Побудуємо знайдені точки на координатній площині \(xOy\).
Ці точки розташовані на певній лінії, накреслимо її. Цю лінію називають параболою.
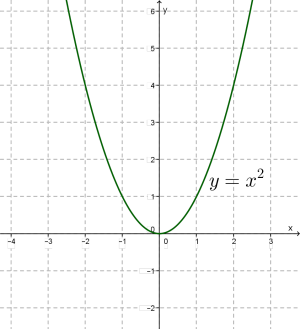
Зверни увагу!
Вісь \(y\) є віссю симетрії параболи . Парабола симетрична щодо осі \(y\). Вісь симетрії ніби розрізає параболу на дві частини, які зазвичай називають вітками параболи.
У параболи є особлива точка, в якій сходяться обидві вітки та яка лежить на осі симетрії параболи — точка \((0; 0). \)Ця точка називається вершиною параболи.
Зазвичай кажуть, що парабола дотикається до осі абсцис.
1. \(y=0\), якщо \(x=0\); \(y>0\) якщо \(x>0\) і якщо \(x<0\)
2.
3. Функція спадає на промені , функція зростає на промені .