Основна властивість числового дробу полягає в тому, що числове значення дробу не зміниться, якщо його чисельник і знаменник помножити або поділити на те ж саме, відмінне від нуля число.
Множення чисельника і знаменника дробу на число називається розширенням дробу (зведенням дробу до нового знаменника), а ділення — скороченням.
|
1.
|
 |
Чисельник і знаменник дробу помножили на \(4\), тобто дріб розширили на \(4\).
(Знаменник також помножили на \(4\)!)
|
|
2.
|
 |
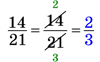Чисельник і знаменник дробу поділили на \(7\), тобто дріб скоротили на \(7\). |
З раціональними дробами можна виконувати ті ж самі дії, що і з числовими дробами: додавання, віднімання, множення, ділення або піднесення до степеня.
Під час виконання цих дій та спрощення результату доводиться використовувати основну властивість раціонального дробу.
Основна властивість раціонального дробу полягає в тому, що значення раціонального дробу не зміниться, якщо його чисельник і знаменник помножити або поділити на той самий вираз, значення якого відмінне від нуля.
|
1.
|
 |
Чисельник і знаменник помножили на одночлен \(2x\); дріб розширили на \(2x\).
(Знаменник також помножили на \(2x\)!)
|
|
2.
|
 |
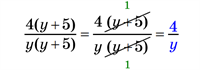Чисельник і знаменник поділили на двочлен \((y + 5)\); дріб скоротили. |
Зверни увагу!
При виконанні дій над раціональними дробами мається на увазі, що всі дії виконуються тільки на області визначення цього дробу (тобто відповідають допустимим значенням змінної). Тож область визначення дробу знаходиться тільки тоді, коли цього вимагає умова завдання.
Приклад:
Скороти:
1. Числа \(26\) і \(169\) мають спільний множник \(13\), тому дріб можна скоротити:
2. Скорочуються степені з однаковими основами:
2.1 Степені і скорочуються діленням на менший степінь :
2.2 Скорочуються рівні множники \(c\). Змінну \(b\) не можна скоротити, оскільки в знаменнику дробу такої змінної немає.
Відповідь. Скоротивши дріб , отримаємо .