Щоб додати (відняти) дроби з однаковими знаменниками, треба додати (відняти) їх чисельники, а знаменник залишити той самий.
Наприклад,
Так само додаються та віднімаються раціональні дроби з однаковими знаменниками:
- при додаванні раціональних дробів з однаковими знаменниками їхні чисельники додаються, а знаменник залишається той самий:
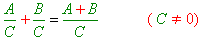
- при відніманні раціональних дробів з однаковими знаменниками від чисельника зменшуваного віднімають чисельник від’ємника, а знаменник залишають той самий:
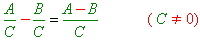
Ці ж правила можна використовувати під час додавання та віднімання кількох дробів з однаковими знаменниками:
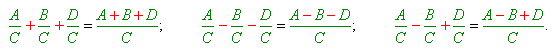
Приклад:
Зверни увагу!
У цих випадках область визначення дробів зазначати не потрібно. Але слід пам'ятати, що будь-яке перетворення дробів має зміст лише для тих значень змінної, які належать області визначення.
Щоб додати або відняти два раціональних дроби, знаменники яких є протилежними виразами, потрібно виконати такі кроки:
- звести дроби до спільного знаменника, тобто один із дробів тотожно перетворити за законом зміни знаків:
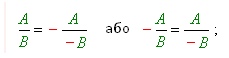
- додати або відняти дроби, застосовуючи правило додавання та віднімання дробів з однаковими знаменниками.
1. Щоб додати дроби та , змінюємо знаки перед дробом та в знаменнику цього дробу на протилежні, потім віднімаємо чисельники обох дробів:
.
2. Щоб відняти дроби та , змінюємо знаки перед дробом та в знаменнику цього дробу на протилежні, потім додаємо чисельники:
Приклад:
Доведи, що значення виразу не залежить від значення змінної в межах області визначення.
Доведення
Тепер усі три дроби мають однакові знаменники. Використовуючи правило додавання та віднімання дробів з однаковими знаменниками, отримуємо:
Отже, значення заданого виразу дорівнює 2 при будь-якому значенні змінної з области визначення, що й треба було довести.
