Щоб додати або відняти звичайні дроби з різними знаменниками, спочатку потрібно знайти спільний знаменник і перетворити знаменники дробів.
Спільний знаменник дробів — це найменше спільне кратне (НСК) знаменників усіх дробів.
НСК — найменше число, яке ділиться на знаменники цих дробів.
Дії над дробами:
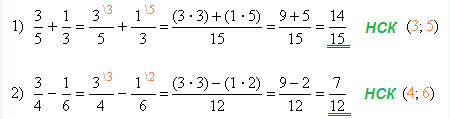
Подібним чином додаються та віднімаються алгебраїчні дроби, знаменниками яких є різні одночлени, наприклад: .
Щоб додати або відняти алгебраїчні дроби, знаменниками яких є різні одночлени, необхідно:
- знайти спільний знаменник;
- визначити додаткові множники для кожного дробу;
- виконати зазначені дії;
- якщо можливо, скоротити отриманий у результаті дріб.
Додаємо дроби:
Спільний знаменник дорівнює , тому що НСК \(( 2 ; 4 ) = 4\), а і \(b\) — степені з найбільшими показниками в обох знаменниках.
Оскільки \(=\) і \(=\) , додатковий множник першого дробу дорівнює \(2\), а додатковий множник другого дробу — \(ab\).
Зверни увагу!
Спільний знаменник дробів — одночлен, коефіцієнт якого дорівнює НСК (найменшому спільному кратному) коефіцієнтів знаменників усіх дробів, що містить усі змінні з найбільшими показниками степенів, які є в знаменниках дробів.
