Функція
Познайомимося з новою функцією:
Коефіцієнт \(k\) може приймати будь-які значення, крім \(k = 0\). Розглянемо спочатку випадок, коли \(k = 1\); отже, спочатку поговоримо про функцію .
Щоб побудувати графік функції , надамо незалежній змінній \(x\) декілька конкретних значень та обчислимо (за формулою ) відповідні значення залежної змінної \(y\).
Щоправда, в цьому випадку зручніше здійснювати обчислення та побудову поступово — спочатку надавати аргументу лише додатних значень, а потім — лише від'ємних.
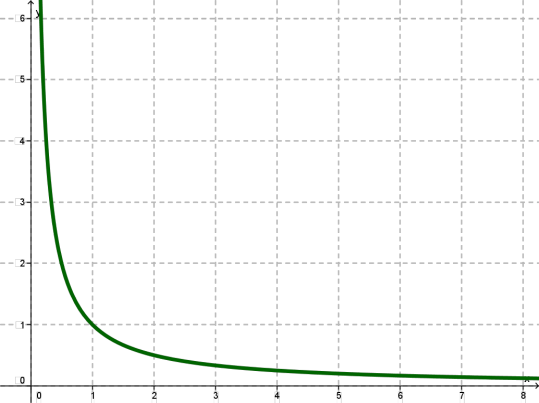
Перший етап
якщо \(x = 2\), то ;
якщо \(x = 4\), то ;
якщо \(x = 8\), то ;
якщо , то \(y = 2\);
якщо , то \(y = 4\);
якщо , то \(y = 8\).
Коротко кажучи, ми склали наступну таблицю:
| \(x\) | \(1\) | \(2\) | \(4\) | \(8\) | |||
| \(y\) | \(1\) | \(2\) | \(4\) | \(8\) |
Побудуємо знайдені точки на координатній площині \(xOy\).
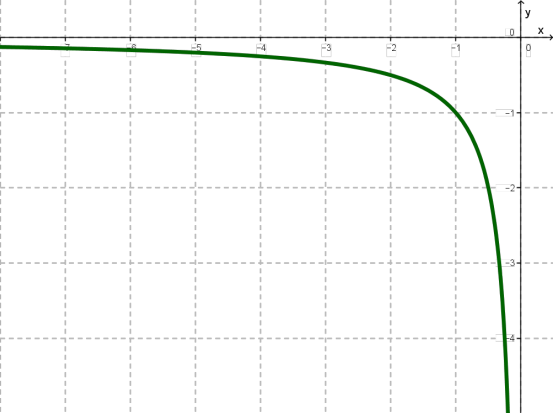
Другий етап
якщо \(x = -1\), то \(y = -1\);
якщо \(x = -2\), то ;
якщо \(x= -4\), то ;
якщо \(x = -8\), то ;
якщо , то \(y = -2\);
якщо , то \(y = -4\);
якщо , то \(y = -8\).
Коротко кажучи, ми склали наступну таблицю:
| \(x\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) | \(-\) | \(-\) | \(-\) |
| \(y\) | \(-1\) | \(-\) | \(-\) | \(-\) | \(-2\) | \(-4\) | \(-8\) |
Побудуємо знайдені точки на координатній площині \(xOy\).
Тепер об'єднаємо два етапи в один, тобто із двох малюнків зробимо один.
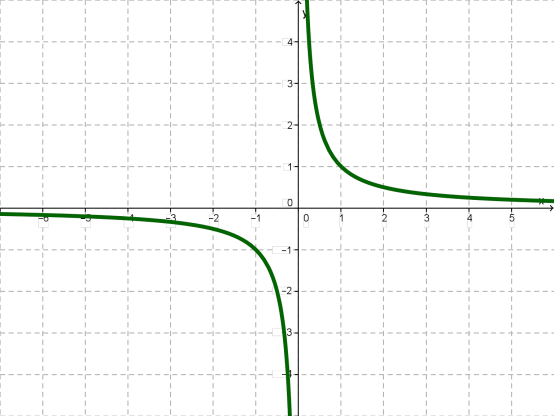
Це і є графіком функції , який називається гіперболою.
Будь-яка пряма, що проходить через початок координат \(O\) та розташована в першому і третьому координатних кутах, перетинає гіперболу в двох точках, які лежать на цій прямій по різні сторони від точки \(O\), але на рівних відстанях від неї. Це властиво, зокрема, точкам \((1; 1)\) і \((- 1; - 1)\), і тощо.
Отже, \(O\) — центр симетрії гіперболи. Говорять також, що гіпербола симетрична відносно початку координат.
По-друге, ми бачимо, що гіпербола складається з двох частин, їх зазвичай називають гілками гіперболи.
По-третє, помічаємо, що кожна гілка гіперболи в одному напрямку підходить все ближче і ближче до осі абсцис, а в іншому напрямку — до осі ординат. У подібних випадках відповідні прямі називають асимптотами.
Отже, графік функції , тобто гіпербола, має дві асимптоти: вісь \(x\) та вісь \(y\).
Якщо уважно проаналізувати побудований графік, можна виявити ще одну геометричну властивість, яка не настільки очевидна, як три попередні (математики звичайно говорять так: «більш тонка властивість»).
Зверни увагу!
Гіпербола має не лише центр симетрії, а й осі симетрії.
Побудуємо пряму \(y = x\).
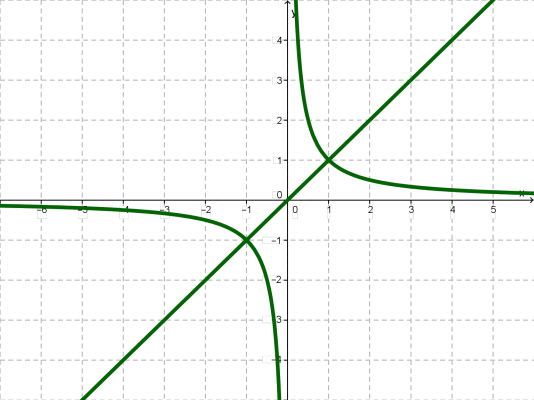
Тепер дивимося: точки розташовані по різні сторони від проведеної прямої, але на рівних відстанях від неї. Вони симетричні відносно цієї прямої.
Те саме можна сказати про точки тощо.
Отже, пряма \(y =x\) — вісь симетрії гіперболи (так само, як і \(y = -x\)).