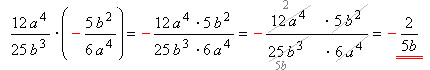Щоб помножити дріб на дріб, треба помножити чисельник на чисельник, а знаменник — на знаменник, і перший добуток записати в чисельнику, а другий — у знаменнику. Таким чином перемножуються кілька дробів.
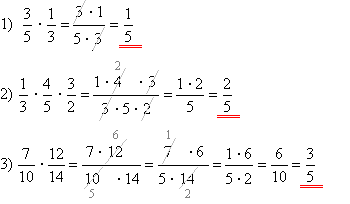
Добуток алгебраїчних дробів тотожно дорівнює дробу, чисельник якого дорівнює добутку чисельників, а знаменник — добутку знаменників перемножуваних дробів.
Якщо можливо, отриманий у результаті дріб скорочують. Окрім того, спільні множники обох дробів потрібно скорочувати вже в процесі множення.
Добуток визначений тільки для тих значень змінних, за яких знаменник дробу не дорівнює нулю.
Тобто, якщо та — два алгебраїчні дроби, де \(A\), \(B\), \(C\), \(D\) — многочлени,
то , де .
Приклад:
Виконай множення
Рішення: добутком додатного та від'ємного чисел є від'ємне число, тому перед добутком ставимо знак «мінус».