Комбінаторика — розділ математики про обчислення кількості різних комбінацій будь-яких елементів.
Приклад:
1. Скільки різних тризначних номерів телефону можна скласти з п'яти цифр? (Відповідь: \(125\))
2. Скількома різними способами можна скласти танцювальну пару, якщо в колективі \(3\) хлопчика і \(4\) дівчинки? (Відповідь: \(12\)).
3. Скількома різними способами можна утворити пару чергових, якщо в класі залишилися Надя, Віка, Саша і Юра? (Відповідь: \(6\)).
4. Скількома різними способами можна вибрати двох учнів (одного - чистити дошку, другого - підмітати підлогу), якщо в класі залишилися Надя, Віка, Саша і Юра? (Відповідь: \(12\))
Один зі способів розв'язання задач комбінаторики - це розглянути всі можливі комбінації елементів, що називається повним перебором варіантів.
Деревоподібна діаграма
Деревоподібна діаграма — один зі способів показати і систематизувати всі розміщення. За допомогою деревовидної діаграми здійснюється повний перебір.
Скільки різних двозначних чисел можна скласти з цифр \(1\), \(2\) і \(3\), якщо кожну використовувати тільки один раз?
Розв'язок:
складається деревоподібна діаграма:
Розв'язок:
складається деревоподібна діаграма:
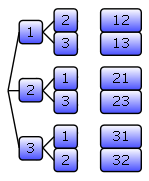
Відповідь: можна скласти \(6\) різних чисел.
Приклад:
Розглянемо 3-й приклад (див. вище):
Скількома різними способами можна утворити пару чергових, якщо в класі залишилися Надія, Вікторія, Назар і Юрій?
Скількома різними способами можна утворити пару чергових, якщо в класі залишилися Надія, Вікторія, Назар і Юрій?
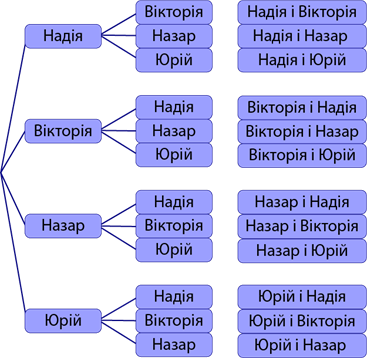
На деревоподібній діаграмі видно, що можна утворити тільки \(6\) пар чергових, оскільки кожна пара повторюється \(2\) рази.
Розглянемо 4-й приклад:
Скількома різними способами можна вибрати двох учнів (одного - чистити дошку, другого - підмітати підлогу), якщо в класі залишилися Надія, Вікторія, Назар і Юрій?
Скількома різними способами можна вибрати двох учнів (одного - чистити дошку, другого - підмітати підлогу), якщо в класі залишилися Надія, Вікторія, Назар і Юрій?
Використовується та ж деревоподібна діаграма, але в даному випадку відповідь буде \(12\) пар, тому що кожна пара з діаграми відрізняється. Якщо дітей поміняти місцями, вони виконують вже інші функції.
За допомогою деревоподібної діаграми були отримані різні результати, тому що в 3 і 4 прикладі були розглянуті різні види комбінацій: поєднання і розміщення.
Такого роду діаграми в подробицях зручно малювати тільки для невеликого числа варіантів, а, наприклад, для сотень комбінацій дерево варіантів цілком не намалюєш. Тоді доводиться діяти по-іншому. Найчастіше при різних підрахунках використовують правило множення:
Для того, щоб знайти число всіх можливих результатів незалежного проведення двох випробувань \(А\) і \(В\), слід помножити число всіх результатів випробування \(А\) і число всіх результатів випробування \(В\).
Таблиця
В окремих випадках для систематизації даних складаються таблиці комбінацій.
Простий ігровий кубик кидається \(2\) рази і отримані пункти помножуються. Скільки різних добутків можна отримати?
Простий ігровий кубик кидається \(2\) рази і отримані пункти помножуються. Скільки різних добутків можна отримати?
| \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | |
| \(1\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(2\) | \(2\) | \(4\) | \(6\) | \(8\) | \(10\) | \(12\) |
| \(3\) | \(3\) | \(6\) | \(9\) | \(12\) |
\(15\)
|
\(18\) |
| \(4\) | \(4\) | \(8\) | \(12\) | \(16\) | \(20\) | \(24\) |
| \(5\) | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
| \(6\) | \(6\) | \(12\) | \(18\) | \(24\) | \(30\) | \(36\) |
Різні добутки - це \(1; 2; 3; 4; 5; 6; 8; 9; 10; 12; 15; 16; 18; 20; 24; 25; 30; 36\) — всього \(18\) різних результатів.
