1. знайти число \(N\) всіма можливими результатами даного випробування;
2. знайти кількість \(N (A)\) тих фіналів випробування, в яких настає подія \(A\);
3. знайти частку , вона і буде дорівнює ймовірності події \(A\)
Розв'язок. Кількість елементарних подій (кількість карт) \(N = 36\). Подія \(A\) - поява карти червової масті. Число випадків, що сприяють появі події \(A\), \(N(A)=9\). Отже,
Імовірністю події \(A\) при проведенні деякого випробування називають відношення числа тих результатів, у результаті яких настає подія \(A\), до загального числа усіх фіналів цього випробування.
Випробування з N наслідками | Множина з N елементів |
Окремий результат випробування | Елемент множини |
Випадкова подія | Підмножина |
Неможлива подія | Порожня підмножина |
Достовірна подія | Підмножина, що збігається з усією множиною |
Імовірність події | Частка елементів підмножини серед всіх елементів множини |
Теорема
Якщо події \(A\) та \(B\) несумісні, тоді ймовірність того, що настане або \(A\) , або \(B\), дорівнює \(P(A) + P(B)\).
Теорема
Для знаходження ймовірності протилежної події, треба від одиниці відняти ймовірність самої події: \(P( A ) = 1-P(A)\).
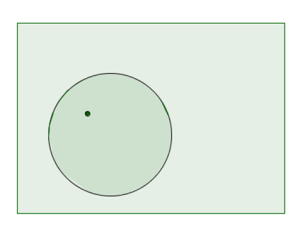
Сформулюємо загальне правило для знаходження геометричних імовірностей.
Якщо площу \(S (A)\) фігури \(A\) поділити на площу \(S (X)\) фігури \(X\), яка цілком містить фігуру \(A\), тоді вийде ймовірність того, що точка, випадково обрана з фігури \(X\), виявиться в фігурі \(A\):
Аналогічно роблять і з множинами на числовій прямій, і з просторовими тілами. Але в цих випадках площі слід замінити або на довжину числових множин, або на обсяги просторових тіл.