Якщо \(k > 0\), тоді функція \(у = kx + m\) зростає на всій числовій прямій.
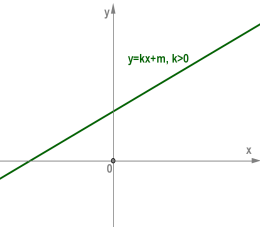
Приклад:
Дослідити на монотонність функцію .
Розв'язання. Графіком лінійної функції є пряма лінія,
для побудови якої достатньо знайти дві точки.
для побудови якої достатньо знайти дві точки.
\(х\) | \(0\) | \(1\) |
\(y\) | \(0\) | \(2\) |
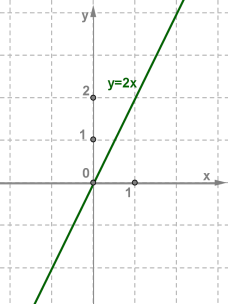
Функція зростає на числовій прямій.
Якщо \(k < 0\), тоді функція \(у = kx + m\) спадає на всій числовій прямій.
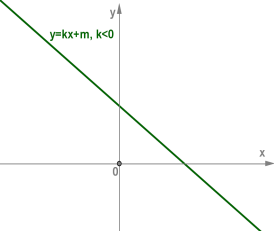
Приклад:
Дослідити на монотонність функцію .
Розв'язання. Графіком лінійної функції є пряма лінія,
для побудови якої достатньо знайти дві точки.
для побудови якої достатньо знайти дві точки.
\(х\) | \(1\) | \(4\) |
\(y\) | \(4\) | \(1\) |
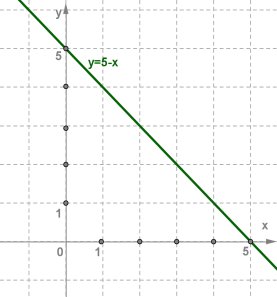
Функція спадає на всій числовій прямій.