Квадратним рівнянням називають рівняння виду , де \(а, b, с\) — будь-які числа (коефіцієнти), .
Використовуючи наші знання про деякі функції та їх графіки, ми вже можемо, не чекаючи систематичного вивчення теми «Квадратні рівняння», розв'язувати деякі квадратні рівняння; ми розглянемо ці способи на прикладі одного квадратного рівняння.
Розв'яжи рівняння .
Перший спосіб.
Побудуємо графік функції .
1. Маємо: \(a = 1, b = -2\), . Отже, вершиною параболи є точка \((1; -4)\), а віссю параболи — пряма \(x = 1\).
2. Візьмемо на осі \(x\) дві точки, симетричні відносно осі параболи, наприклад, точки \(x = -1\) та \(x = 3\). Маємо \(f(-1) = f(3) = 0\). Побудуємо на координатній площині точки \((-1; 0)\) та \((3; 0)\).
3. Через точки \((-1; 0), (1; -4), (3; 0)\) проводимо параболу.
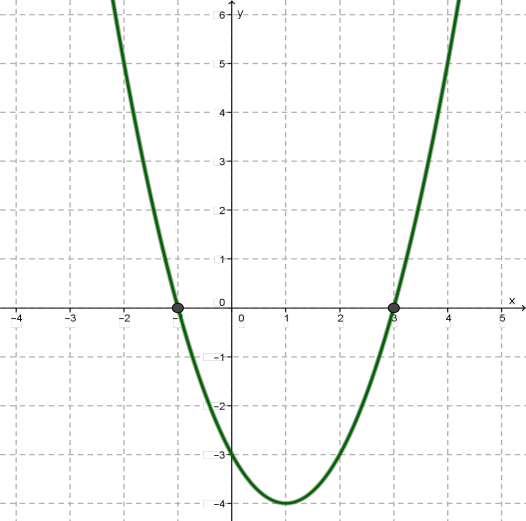
Коренями рівняння є абсциси точок перетину параболи з віссю \(х\); отже, корені рівняння такі: .
Другий спосіб.
Зведемо рівняння до вигляду . Побудуємо в одній системі координат графіки
функцій: .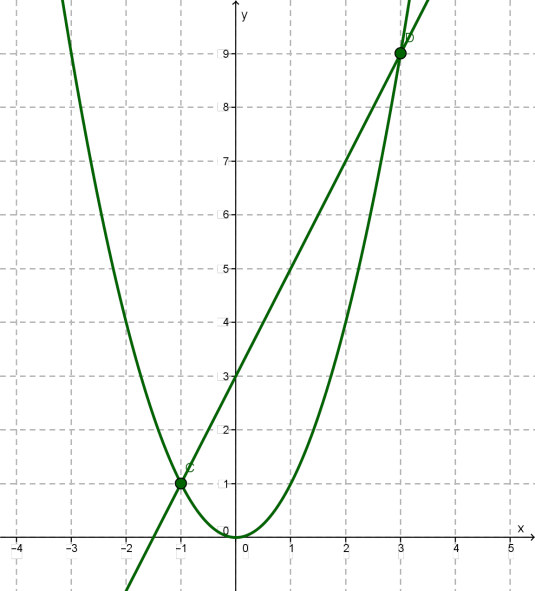
Вони перетинаються в двох точках \(C(- 1; 1)\) та \(D(3; 9)\). Коренями рівняння є абсциси точок \(C\) та \(D\), отже, .
Третій спосіб.
Зведемо рівняння до вигляду . Побудуємо в одній системі координат графіки функцій: .
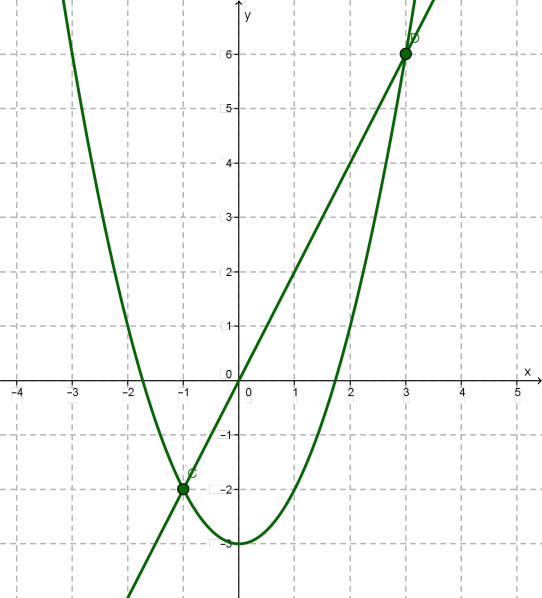
Вони перетинаються в двох точках \(C(-1; - 2)\) та \(D(3; 6)\). Коренями рівняння є абсциси точок \(C\) та \(D\), тому .
Четвертий спосіб.
Побудуємо в одній системі координат параболу і пряму \(y = 4\).
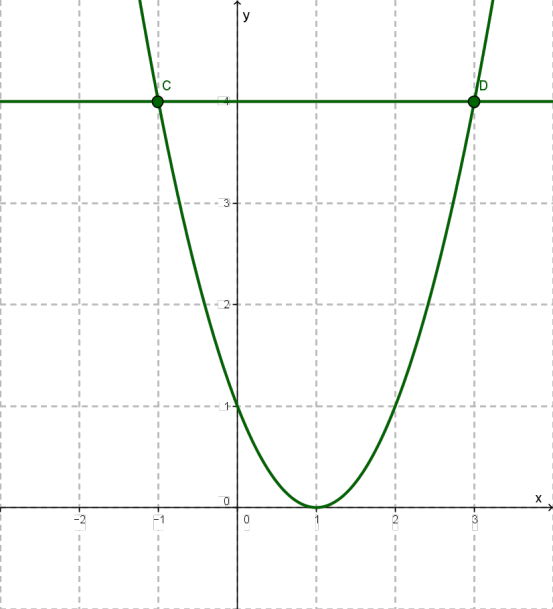
Вони перетинаються в двох точках \(C(-1; 4)\) та \(D(3; 4)\). Коренями рівняння є абсциси точок \(C\) та \(D\), тому .
П'ятий спосіб.
Поділивши почленно обидві частини рівняння на \(x\), отримаємоПобудуємо в одній системі координат гіперболу і пряму \(y = x - 2\).
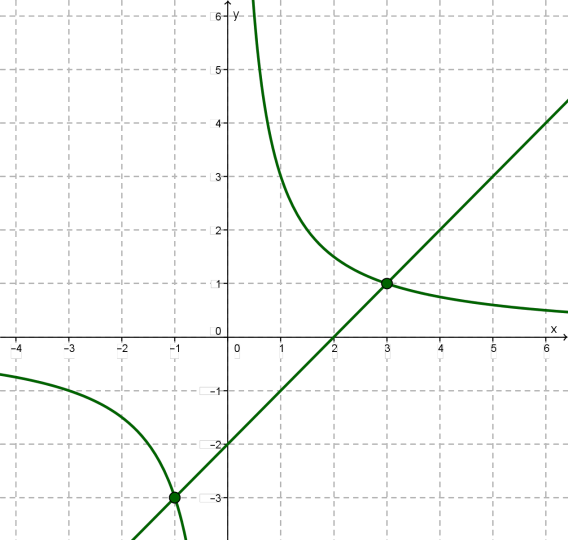
Вони перетинаються в двох точках \(A (-1; -3)\) та \(B(3; 1)\). Коренями рівняння є абсциси точок \(A\) та \(B\), отже, .
Таким чином, квадратне рівняння ми розв'язали графічно п'ятьма способами.