Пряму \(l\), на якій обрано початкову точку \(О\) (початок відліку), масштаб (одиничний відрізок, тобто відрізок, довжина якого вважається рівною \(1\)) і додатний напрямок, називають координатною прямою або координатною віссю.
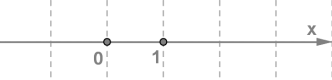
Кожному числу на координатній прямій відповідає єдина точка.
Приклад:
Числу \(2\) відповідає точка \(А\), яка віддалена від початку відліку, тобто від точки \(О\), на відстань, рівну \(2\) (у заданому масштабі), і відкладена від точки \(О\) в заданому (додатному) напрямку.
Числу \(-2\) відповідає точка \(М\), яка віддалена від початку відліку, тобто від точки \(О\), на відстань, рівну \(2\) (у заданому масштабі), і відкладена від точки \(О\) у від'ємному напрямку, тобто в напрямку, протилежному заданому.
Числу \(-2\) відповідає точка \(М\), яка віддалена від початку відліку, тобто від точки \(О\), на відстань, рівну \(2\) (у заданому масштабі), і відкладена від точки \(О\) у від'ємному напрямку, тобто в напрямку, протилежному заданому.
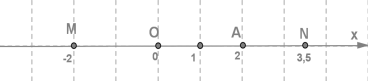
Правильно і зворотне, тобто точка \(N \), віддалена від точки \(О\) на відстань \(3,5\) в додатному (заданому) напрямку, відповідає числу \(3,5\), а точка \(М\), віддалена від точки \(О\) на відстань \(2\) у від'ємному напрямку, відповідає числу \(-2\).
Зазначені числа називають координатами відповідних точок.
Отже, точка \(A\) має координату \(2\);
точка \(N\) має координату \(3,5\);
точка \(М\) має координату \(-2\);
точка \(О\) має координату \(0\).
Записуємо це так: \(A\)(\(2\)); \(N\)(\(3,5\)); \(М\)(\(-2\)); \(О\)(\(0\)).
Можна знайти відстань між двома точками на координатній прямій. Маємо дві точки: \(A (a)\) і \(B (b)\). Відстань \(AB =\) .
Використовуючи цю формулу, отримаємо
Координатна пряма дає можливість вільно переходити з алгебраїчної мови на геометричну та назад.
1. Нехай на координатній прямій відзначено точку \(a\).
Зазначимо (зафарбуємо) на координатній прямій усі точки, розташовані праворуч від точки \(a\).
Зазначимо (зафарбуємо) на координатній прямій усі точки, розташовані праворуч від точки \(a\).

Цю множину точок (чисел) називають відкритим проміжком і позначають .
Це характеризується нерівністю , де \(x\) — будь-яка точка відкритого проміжку.
Якщо точку \(a\) приєднати до відкритого проміжку, тоді вийде проміжок.
Якщо точку \(a\) приєднати до відкритого проміжку, тоді вийде проміжок.

Проміжок позначаємо і характеризуємо нерівністю .
2. Зазначимо (зафарбуємо) на координатної прямої усі точки, розташовані ліворуч від точки \(a\),
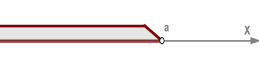
отриману множину точок (чисел) також називають відкритим проміжком, позначають і характеризують нерівністю .
Якщо точку \(a\) приєднати до відкритого проміжку, тоді також вийде проміжок.

Проміжок позначаємо і характеризуємо нерівністю .
3. Відзначимо на координатній прямій точки \(a\) і \(b\), причому \(a < b\) (тобто точка \(a\) розташована на прямій ліворуч від точки\(b\)).
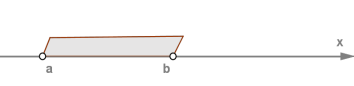
Отриману множину точок (чисел) називають інтервалом, позначають \((a; b)\) і характеризують подвійною нерівністю \(a <x <b\).
Якщо до інтервалу \((a; b)\) додати його кінці,
Якщо до інтервалу \((a; b)\) додати його кінці,
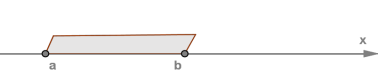 ,
, тоді вийде відрізок , який характеризується нестрогою подвійною нерівністю .
4. Якщо до інтервалу \((a; b)\) додати один з його кінців
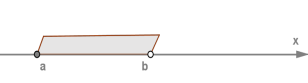
(праворуч або ліворуч),
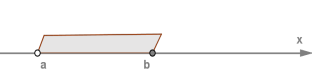
тоді вийде напівінтервал, який позначають чи і характеризують за допомогою подвійних нерівностей: і .
Отже, введено п'ять нових термінів: проміжок, відкритий проміжок, інтервал, відрізок, напівінтервал. Загальна їх назва — числові проміжки.
Сама координатна пряма — також числовий проміжок, який позначають
Сама координатна пряма — також числовий проміжок, який позначають
.
