Виміряти будь-яку величину — це означає порівняти її з однорідною величиною, прийнятою за одиницю.
Будь-яке вимірювання може бути виконано з більшою або меншою точністю.
Як приклад розглянемо вимірювання довжини бруска лінійкою із сантиметровими поділками.
Як приклад розглянемо вимірювання довжини бруска лінійкою із сантиметровими поділками.
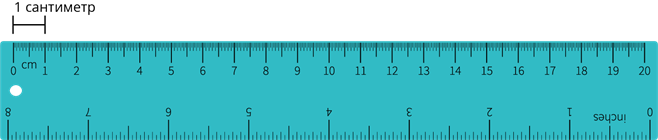
Спочатку визначимо ціну поділки лінійки. Вона буде дорівнювати \(1\) см. Якщо лівий кінець бруска поєднати з нульовим штрихом, то правий буде перебувати між \(9\) та \(10\) штрихами, але ближче до \(10\). Яке ж з цих двох значень необхідно прийняти за довжину бруска? Очевидно, те, яке ближче до істинного значення, тобто \(10\) см. Вважаючи, що довжина бруска \(10\) см, ми допустимо неточність, тому що брусок трохи коротший за \(10\) см.
У фізиці неточність, що допускається при вимірюванні називають похибкою вимірювань.

Для більш точних вимірювань можна скористатися штангенциркулем із ціною поділки \(0,1\) мм або \(0,05\) мм.

З цього прикладу видно, що точність вимірювань залежить від ціни поділки шкали приладу.
Чим менша ціна поділки, тим більше точність вимірювання.
Точність вимірювання залежить від правильного застосування вимірювального приладу, розташування очей до початку відліку на приладі.
Унаслідок недосконалості вимірювальних приладів і недосконалості в розвитку наших органів чуттів при будь-якому вимірюванні виходять лише наближені значення, кільтрохи більші або менші істинного значення вимірюваної величини.
Під час виконання лабораторних робіт або просто вимірювань необхідно вважати, що:
Похибка вимірювань дорівнює половині ціни поділки шкали вимірювального приладу.
Під час запису величин, з урахуванням похибки, необхідно користуватися формулою: ,
де \(A\) — величина, що вимірюється, \(a\) — результат вимірювань, — похибка вимірювань ( — грецька буква «дельта»).
де \(A\) — величина, що вимірюється, \(a\) — результат вимірювань, — похибка вимірювань ( — грецька буква «дельта»).