Спортсмен, спідометр який має велосипед, рухається по трасі. Швидкість руху, яку показує спідометр у будь який момент часу, дорівнює \(5м/с\). Як описати рух цього спортсмена і взагалі будь-якого тіла з адопомогою графіків?
Побудуємо графік залежності шляху, який долає велосипедист від часу спостереження — графік шляху.
Для побудови графіка заповнимо табицю відповідних значень часу \(t\ \)руху спортсмена та шляху \(l\), який він долає за цей час.
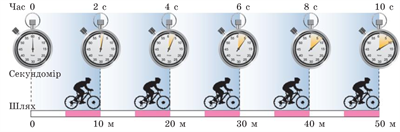
Велосипедист рухається рівномірно прямолінійно: за будь-які рівні інтервали часу він долає однаковий шлях.
В момент часу спостереження \(t = 0\) та \(l = 0\). За \(2\) секунди велосипедист долає \(10\ \)м: \(l = v·t = 5\ м/с·2\ с =10\ м\).
| \(t\), с | \(0\) | \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
| \(l\), м | \(0\) | \(10\) | \(20\) | \(30\) | \(40\) | \(50\) |
Проведемо дві взаємно перпендикулярні осі. На горизонтальній осі — осі абсцис — відкладемо час руху велосипедиста, а на вертикальній — осі ординат — відкладемо шлях в метрах.
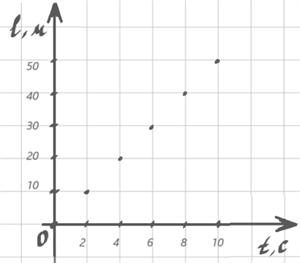
Побудуємо точки з координами, що відповідають даним з таблиці \((0;0)\), \((2;10)\) й т.д.
З'єднавши побудовані точки лінією, й отримаємо відрізок прямої — графік шляху велосипедиста.
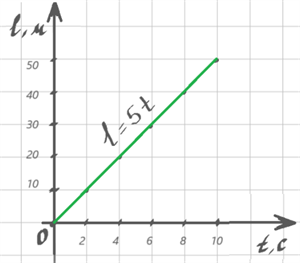
Рівність \(l = 5t\) — рівняння залежності шляху, який долає велосипедист, від часу спостереження.
У разі рівномірного руху графік шляху — це завжди відрізок прямої, нахиленої під певним кутом до осі часу. Тому для побудови графіка шляху достатньо знайти шлях \(l\) для двох значень часу \(t\) і через отримані дві точки провести відрізок прямої.
Про що можна дізнатись за графіком шляху
Графік шляху дає багато корисної інформації. За графіком шляху можна:
1) дізнатися про характер руху тіла;
2) визначити шлях, який долає тіло за певний інтервал часу;
3) визначити швидкість руху тіла;
4) порівняти швидкості руху тіл.
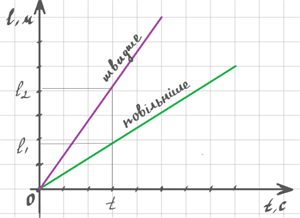
Зверни увагу!
Чим більша швидкість руху тіл, тим більший кут між графіком шляху та віссю часу.
Розглянемо приклад:
Графік швидкості рівномірного руху тіла
Будуємо графік швидкості рівномірного руху спортсмена від часу спостереження — графік швидкості руху.
Для побудови графіка заповнимо таблицю відповідних моментів часу \(t\) руху та швидкості \(v\) руху , яку він мав у ці моменти:
| \(t\), с | \(0\) | \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
| \(v\), м/с | \(5\) | \(5\) | \(5\) | \(5\) | \(5\) | \(5\) |
На осі асцис відкладемо час руху в секундах, на осі ординат — швидкість руху в метрах в секунду.
Будуємо точки \((0;5)\), \((2;5)\), ... абсциси яких відповідають часу руху спортсмена, ординати — швидкості його руху.
З'єднавши побудовані точки лінією, й отримаємо відрізок прямої, паралельний осі часу — графік швидкості руху велосипедиста.
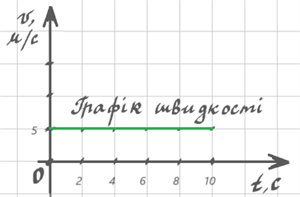
За графіком швидкості можна:
1) дізнатися, як рухалося тіло;
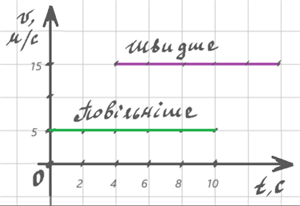
2) визначити й порівняти швидкості руху тіл;
3) знайти шлях, який долало тіло за певний інтервал часу.
Зверни увагу!
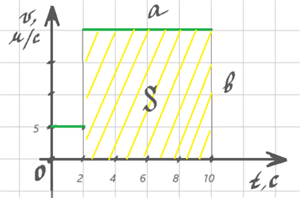
Для будь-якого руху числове значення шляху, який подолало тіло, дорівнює числовому значенню площі фігури під графіком швидкості руху цього тіла.
Джерела:
Баряхтар В.Г. Фізика 7 клас — 2024 р.
