За допомогою градусної сітки на географічній карті та глобусі можна визначати відстані між географічними об'єктами.
Усі меридіани мають однакову довжину, довжина \(1\)° дуги меридіанів становлять \(111,3\) км.
Довжина \(1\)° паралелі зменшується у напрямку від екватора до полюсів, і відповідно відрізняється на різних широтах. Найдовшою паралеллю є екватор, найкоротшими — полюси.

Визначення відстаней по паралелям
На початку знаходимо географічну довготу об'єктів. Далі визначаємо відстань між об'єктами у градусах.
Зверни увагу!
Якщо об'єкти розташовані в межах однієї півкулі, від більшого показника довготи віднімаємо менший. Якщо об'єкти розташовані у різних півкулях, то показники довгот додаємо.
Знайдену відстань між об'єктами у градусах множимо на показник \(1\)° дуги паралелей.
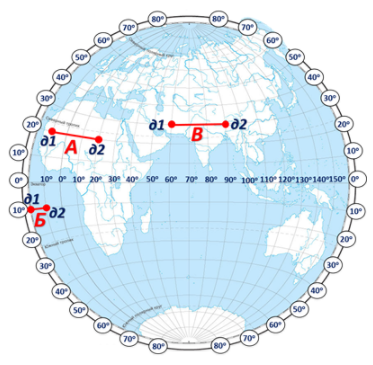
Приклад:
А= (д\(1\)+ д\(2\)) ⋅ \(104,6\) (довжина \(1\)° на широті \(20\)°) = (\(10\)°+ \(20\)°) ⋅ \(104,6\)= \(30\)° ⋅ \(104,6\)= \(3138\) км.
Б= (д\(1\) – д\(2\)) ⋅ \(109,6\)= (\(20\)°– \(10\)°) ⋅ \(109,6\)= \(10\)°⋅ \(109,6\)= \(1096\) км.
В= (д\(2\) – д\(1\)) ⋅ \(96,5\)= (\(90\)°– \(60\)°) ⋅ \(96,5\)= \(30\)°⋅ \(96,5\)= \(2895\) км.
Визначення відстаней по меридіанам
На початку знаходимо географічну широту об'єктів. Далі визначаємо відстань між об'єктами у градусах.
Зверни увагу!
Якщо об'єкти розташовані в межах однієї півкулі, то від більшого показника широти віднімаємо менший. Якщо об'єкти розташовані у різних півкулях, то показники широт додаємо.
Знайдену відстань між об'єктами у градусах множимо на показник \(1\)° дуги меридіанів, на \(111\) км.
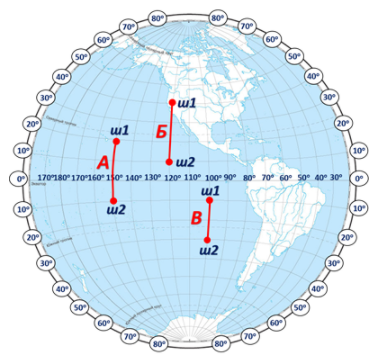
Приклад:
А= (ш\(1\)+ ш2) ⋅ \(111\ \)= (\(20\)°+ \(10\)°) ⋅ \(111\)= \(30\)°⋅ \(111\)= \(3330\) км.
Б= (ш\(1\) – ш2) ⋅ \(111\)= (\(40\)°– \(10\)°) ⋅ \(111\)= \(30\)°⋅ \(111\)= \(3330\) км.
В= (ш\(2\) – ш1) ⋅ \(111\)= (\(30\)°– \(10\)°) ⋅ \(111\)= \(20\)°⋅ \(111\)= \(2220\) км.
