Як відомо з аксіом геометрії, якщо площини мають одну спільну точку, то вони перетинаються по прямій, що проходить через цю точку. Отже, дві площини або перетинаються, або не перетинаються.
Площини, що не перетинаються, називаються паралельними.
Паралельні площини і позначаються
Приклад:
Будь-яка конструкція з підлогою, стелею та стінами дає нам уявлення про паралельні площини — підлога і стеля як дві паралельні площини, бокові стіни як паралельні площини.



Ознака паралельності площин.
Якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом прямим, що перетинаються, другої площини, то ці площини паралельні.
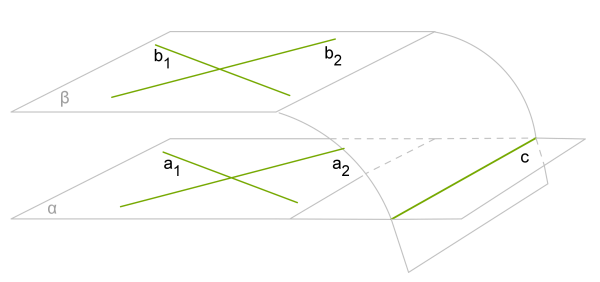
Доведення.
Нехай і — дані площини, і — прямі, що перетинаються в площині , а і відповідно паралельні їм прямі в площині .
Припустимо, що площини і не паралельні, тобто вони перетинаються по деякій прямій \(c\).
Пряма паралельна прямій , отже вона паралельна і площині .
Пряма паралельна прямій , отже, вона паралельна і площині (ознака паралельності прямої і площини).
Пряма \(c\) лежить у площині , отже принаймні одна з прямих або перетинає пряму \(c\), тобто має з нею спільну точку. Але пряма \(c\) також лежить і в площині , це означає, що перетинаючи пряму \(c\), пряма або перетинає площину , чого бути не може, оскільки прямі і паралельні площині .
Таким чином, площини і не перетинаються, тобто вони паралельні.
Властивості паралельних площин.
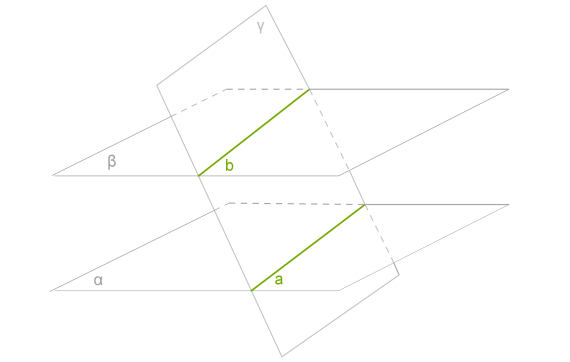
Доведення.
Нехай і — паралельні площини, а — площина, що перетинає їх.
Площина перетинається з площиною по прямій \(a\).
Площина перетинається з площиною по прямій \(b\).
Лінії перетину \(a\) і \(b\) лежать в одній площині і тому можуть бути або такими, що перетинаються, або паралельними. Але, оскільки вони лежать у двох паралельних площинах, вони не можуть мати спільних точок. Очевидно, вони паралельні.
Теорема 2. Відрізки паралельних прямих, які містяться між паралельними площинами, рівні.
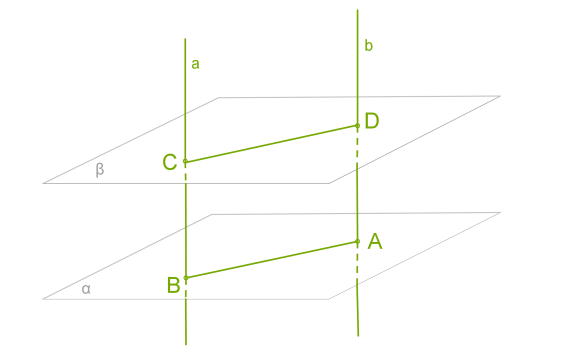
Доведення.
Нехай і — паралельні площини, а \(a\) і \(b\) — паралельні прямі, що перетинають їх.
Через прямі \(a\) і \(b\) можна провести площину — ці прямі паралельні, отже визначають площину, і до того ж лише одну.
Проведена площина перетинається з площиною по прямі \(AB\), а з площиною по прямій \(CD\).
З попередньої теореми \(AB\) і\(CD\) паралельні. Чотирикутник \(ABCD\) є паралелограмом (у нього протилежні сторони паралельні). А якщо це паралелограм, то протилежні сторони у нього рівні, тобто \(BC = AD\).
