1. Паралельні прямі в просторі
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються.
Паралельність прямих \(a\) і \(b\) позначається так: .
Teорема 1. Через дві паралельні прямі можна провести площину, і до того ж тільки одну.
Доведення:
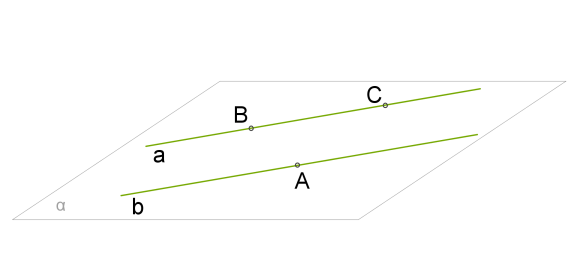
1. Якщо прямі \(a\) і \(b\) паралельні, із визначення випливає, що через них можна провести площину .
2. Щоб довести, что така площина тільки одна, на прямій \(a\) позначаємо точки \(B\) і \(C\), а на прямій \(b\) — точку \(A\).
3. Оскільки через три точки, що не лежать на одній прямій, можна провести тільки одну площину (2 аксіома), то — єдина площина, якій належать прямі \(a\) і \(b\).
Теорема 2. Через будь-яку точку простору поза даною прямою можна провести пряму, паралельну даній прямій, і до того ж тільки одну.
Доведення:
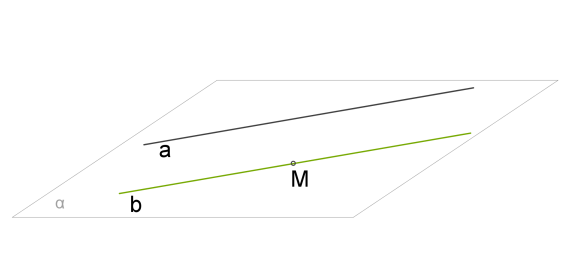
1. Через дану пряму \(a\) і точку \(M\), що не лежить на прямій, проводимо площину .
2. Така площина тільки одна, оскільки через пряму і точку, що не лежить на прямій, можна провести площину, до того ж тільки одну.
3. А в площині через точку \(M\) можна провести тільки одну пряму \(b\), що паралельна прямій \(a\).
Теорема 3. Якщо одна з двох паралельних прямих перетинає дану площину, то й інша пряма перетинає цю площину.
(1. рис.)
(2. рис.)
Доведення:
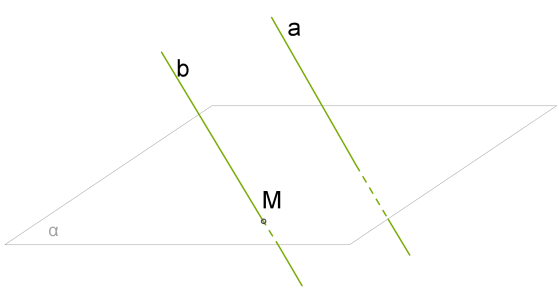
Розглянемо дві паралельні прямі \(a\) і \(b\) і припустимо, що пряма \(b\) перетинає площину в точці \(M\) (1. рис.).
З 1-ої теореми відомо, що через паралельні прямі \(a\) і \(b\) можна провести тільки одну площину .
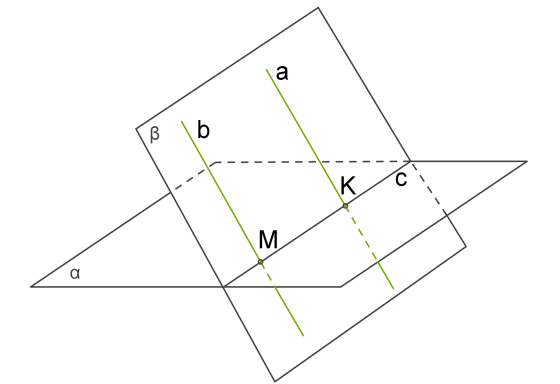
Оскільки точка \(M\) розташована на прямій \(b\), то \(M\) також належить площині (2. рис.). Якщо площини і мають спільну точку \(M\), то у цих площин є спільна пряма \(c\), яка є прямою перетину цих площин (4 аксіома).
Прямі \(a\), \(b\) і \(c\) розміщені в площині .
Якщо в цій площині одна з паралельних прямих \(b\) перетинає пряму \(c\), то друга пряма \(a\) також перетинає \(c\).
Точку перетину прямих \(a\) і \(c\) позначимо за \(K\).
Оскільки точка \(K\) розміщена на прямій \(c\), то \(K\) розміщена в площині і буде єдиною спільною точкою прямої \(a\) і площини .
Отже, пряма \(a\) перетинає площину в точці \(K\).
Теорема 4. Дві прямі, паралельні третій, паралельні між собою.
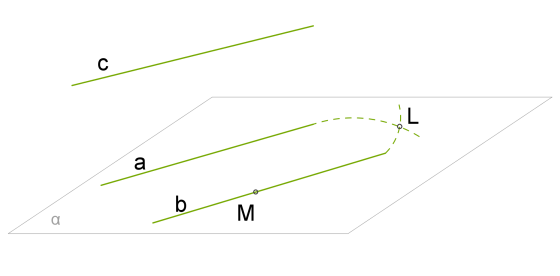
Нехай
Доведемо, що
Доведення:
Оберемо точку \(M\) на прямій \(b\).
Через точку \(M\) і пряму \(a\), яка не містить цю точку, можна провести тільки одну площину (Через пряму і точку, що не лежить на ній, можна провести тільки одну площину).
Можливі два випадки:
1) пряма \(b\) перетинає площину ;
2) пряма \(b\) лежить у площині .
Нехай пряма \(b\) перетинає площину .
Отже, пряма \(c\), що паралельна прямій \(b\), також перетинає площину . Оскільки , то виходить, що \(a\) також перетинає цю площину. Але пряма \(a\) не може одночасно перетинати площину і лежати у площині . Маємо суперечність, отже, припущення, що пряма \(b\) перетинає площину , є неправильним.
Отже, пряма \(b\) лежить у площині .
Тепер треба довести, що прямі \(a\) і \(b\) паралельні.
Нехай прямі \(a\) і \(b\) мають спільну точку \(L\).
Це означає, що через точку \(L\) проведено дві прямі \(a\) і \(b\), паралельні прямій \(c\). Але відповідно до другої теореми це неможливо. Тому припущення неправильне, і прямі \(a\) і \(b\) не мають спільних точок.
Оскільки прямі \(a\) і \(b\) містяться в одній площині і не мають спільних точок, то вони паралельні.
Уся множина прямих у просторі, які паралельні даній прямій, називається пучком паралельних прямих.
Висновки:
1) Будь-які дві прямі з пучка паралельних прямих паралельні між собою.
2) Паралельності прямих у просторі притаманна транзитивність:
Приклад:
Одна сторона параллелограма перетинає площину. Доведіть, що пряма, що містить протилежну сторону паралелограма, також перетинає цю площину.
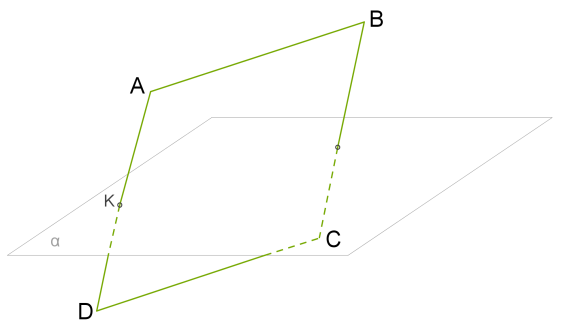
Припустимо, що у паралелограма \(ABCD\) сторона \(AD\) перетинає площину в точці \(K\).
Оскільки протилежні сторони паралелограма паралельні, то, відповідно до третьої теореми, пряма, що містить сторону \(CD\), також перетинає площину .
2. Паралельність прямої та площини.
1) пряма лежить в площині;
2) пряма і площина мають тільки одну спільну точку (пряма і площина перетинаються);
3) пряма і площина не мають спільних точок.
Пряма і площина називаються паралельними, якщо вони не мають спільних точок.
Теорема 5 «Ознака паралельності прямої і площини».
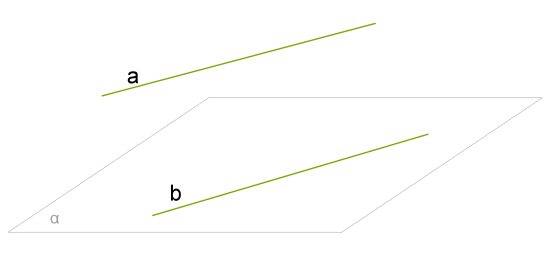
Якщо пряма, що не лежить у даній площині, паралельна будь-якій прямій з цієї площини, то ця пряма паралельна даній площині.
Якщо пряма, що не лежить у даній площині, паралельна будь-якій прямій з цієї площини, то ця пряма паралельна даній площині.
Доведення:
Доведення проведемо від супротивного. Нехай \(a\) не паралельна площині , тоді пряма \(a\) перетинає площину в якійсь точці \(A\). Причому \(A\) не лежить на \(b\), оскільки . Відповідно до ознаки прямих, що перетинаються, прямі \(a\) і \(b\) перетинаються.
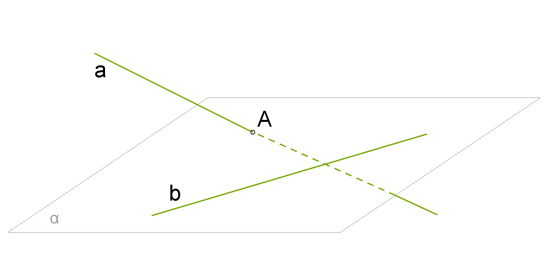
Доведення проведемо від супротивного. Нехай \(a\) не паралельна площині , тоді пряма \(a\) перетинає площину в якійсь точці \(A\). Причому \(A\) не лежить на \(b\), оскільки . Відповідно до ознаки прямих, що перетинаються, прямі \(a\) і \(b\) перетинаються.

Ми дійшли до суперечності. Оскільки , вони не можуть перетинатися. Отже, пряма \(a\) паралельна площині .
Зверни увагу!
Наступні дві теореми дуже часто використовуються при розв'язанні задач.
Теорема 6.
Якщо площина проходить через дану пряму \(a\), паралельну площині , і перетинає цю площину по прямій \(b\), то .
Якщо площина проходить через дану пряму \(a\), паралельну площині , і перетинає цю площину по прямій \(b\), то .
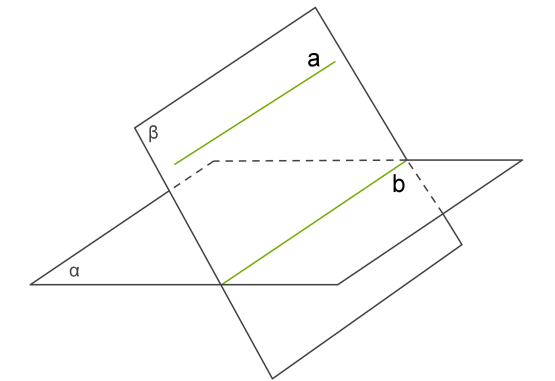
Зверни увагу!
Пряму \(b\) іноді називають відбитком площини на площині.
Теорема 7.
Якщо одна з двох паралельних прямих є параллельною даній площині , то друга пряма або є параллельною цій площині, або лежить у цій площині.
Якщо одна з двох паралельних прямих є параллельною даній площині , то друга пряма або є параллельною цій площині, або лежить у цій площині.