Площиною переріза багатогранника можна назвати будь-яку площину, по обидва боки якої знаходяться точки багатогранника.
Січна площина перетинає грані багатогранників по відрізках.
Багатокутник, сторонами якого є такі відрізки, називається перерізом багатогранника.
Оскільки у тетраедра \(4\) грані, то перерізом тетраедра може бути трикутник (Рис. 7.) або чотирикутник (Рис. 8.)
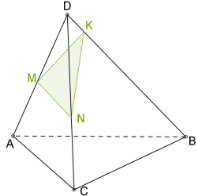
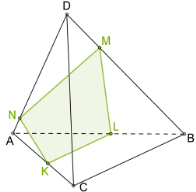
Рис. 7. Рис. 8.
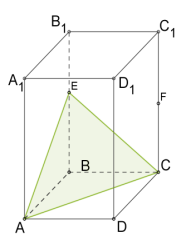
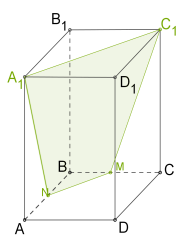
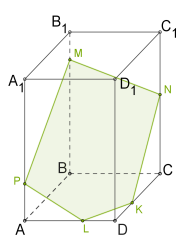
У паралелепіпеда \(6\) граней, тому перерізом цього багатогранника може бути трикутник (Рис. 9.), чотирикутник ( Рис. 10. ),
п'ятикутник (Рис. 11. ) або шестикутник (Рис. 12.).
 |
 |
 |
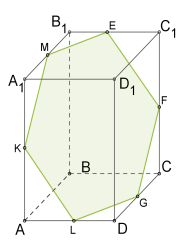 |
| Рис. 9. | Рис. 10. | Рис. 11. | Рис. 12. |
При побудові переріза треба згадати такі знання з попередніх тем:
1. Якщо дві точки прямої належать площині, то пряма знаходиться в цій площині.
2. Якщо дві площини мають спільну точку, то ці площини перетинаються по прямій.
3. Якщо площина перетинає дві паралельні площини, то лінії перетину паралельні.
Приклад:
Задача
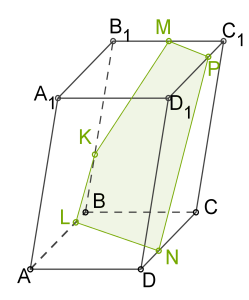
Побудувати переріз паралелепіпеда площиною, яка проходить через точки\(K\), \(M\) і \(N\).
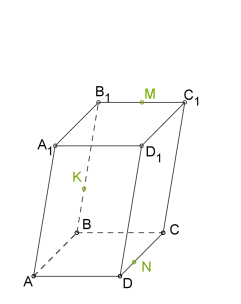
1. Проводимо \(MK\), оскільки обидві точки знаходяться в одній площині.
2. непаралельних прямі в одній площині перетинаються.
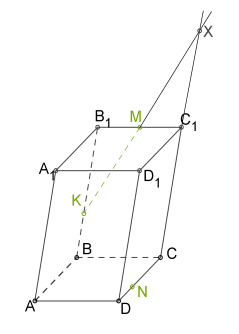
3. Проводимо \(XN\), оскільки обидві точки знаходяться в одній площині.
4.
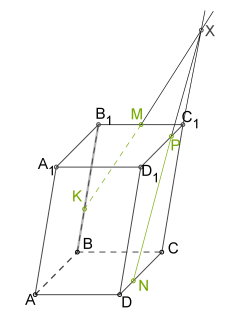
5. Проводимо \(MP\), оскільки обидві точки знаходяться в одній площині.
6. Через точку \(N\) у площині основи оскільки лінії перетину паралельних площин з третьої площиною повинні бути паралельні.
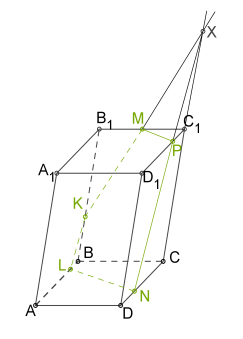
7. З'єднаємо \(N\) і \(L\) і отримаємо переріз\(MPNLK\).