Якщо пряма, проведена на площині через основу похилої, перпендикулярна її проекції, то вона перпендикулярна й самій похилій.
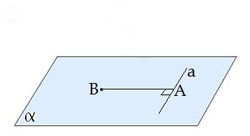 \(a\)\(AB\) | 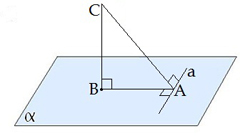 |
Справедлива також зворотня теорема:
Якщо пряма на площині перпендикулярна похилій, то вона перпендикулярна і проекції похилої.
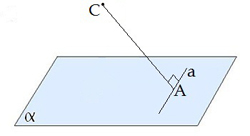 \(a\)\(AC\) |  |
Із вершини \(S\) до площини квадрата \(ABCD\) проведено перпендикуляр \(BS\) і похилі \(SA\), \(SC\) і \(SD\).
Назви всі прямокутні трикутники з вершиною \(S\), обґрунтуй свою відповідь.
Назви всі прямокутні трикутники з вершиною \(S\), обґрунтуй свою відповідь.
Малюнок:
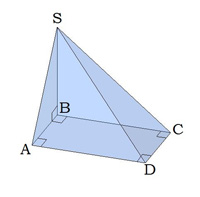 \(ABCD\) квадрат, всі кути якого дорівнюють градусів. 1. Грань \(ASB\) — прямокутний трикутник, 2. Грань \(BSC\) — прямокутний трикутник, тому що \(BS\) — перпендикуляр до площини. |
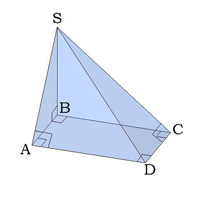 3. Грань \(DSC\) — прямокутний трикутник, за теоремою про три перпендикуляри: отже, \(SCD =\) 4. Грань \(ASD\) — прямокутний трикутник, за теоремою про три перпендикуляри: отже, \(SAD =\) . |
