Одне з визначень компланарних векторів каже:
Вектори, які паралельні одній площині або лежать на одній площині, називаються компланарними векторами.
Три вектори називаються компланарними, якщо вони, приведені до спільного початку та лежать в одній площині.
Зверни увагу!
Завжди можливо знайти площину, паралельну двом довільним векторам, тому будь-які два вектори завжди компланарні.
Якщо з трьох векторів два колінеарні, то очевидно, що ці три вектори компланарні.
Якщо з трьох векторів два колінеарні, то очевидно, що ці три вектори компланарні.
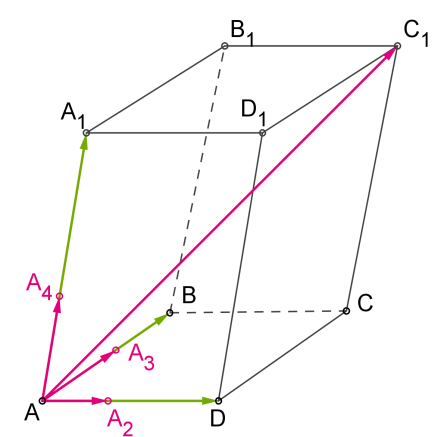
Усі вищезазначені випадки легко розглянути, якщо розташувати вектори на ребрах паралелепіпеда.
1. Будь-які два вектори знаходяться в одній площині, але в одній площині можна розташувати і вектори , і , тобто ці вектори компланарні.
Також компланарні вектори , і , тому що два з цих векторів паралельні. Легко уявити, що якщо привести їх до спільного початку, то вектор співпаде з вектором .
Також компланарні вектори , і , тому що два з цих векторів паралельні. Легко уявити, що якщо привести їх до спільного початку, то вектор співпаде з вектором .
2. Наприклад, вектори , і не компланарні, тому що їх не можна розташувати в одній і тій же площині.
Ознака компланарності трьох векторів:
Нехай вектори і не колінеарні. Якщо для вектора існує єдина пара дійсних чисел \(x\) і \(y\), така, що , то вектори , і
компланарні.
компланарні.
Справедливо і зворотне твердження:
Якщо три вектори , і компланарні і вектори і не колінеарні, то вектор можна розкласти за векторами і одним єдиним чином.
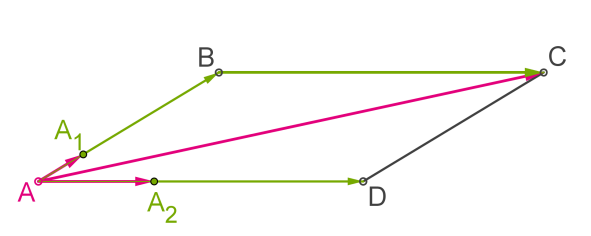
Якщо розкласти вектор за векторами і , то це можна зробити одним єдиним чином
Закон паралелепіпеда
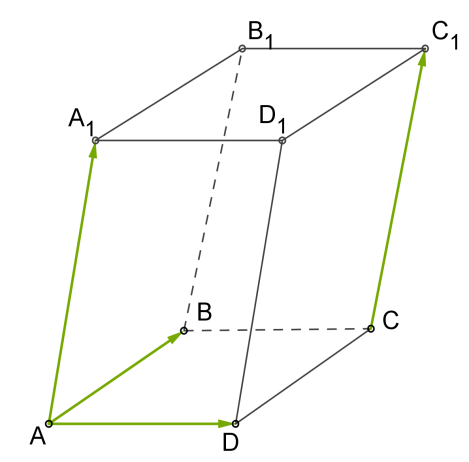
Якщо три вектори не компланарні, то для їх додавання у просторі застосовують закон паралелепіпеда.
1. Вектори зводять до спільного початку \(A\);
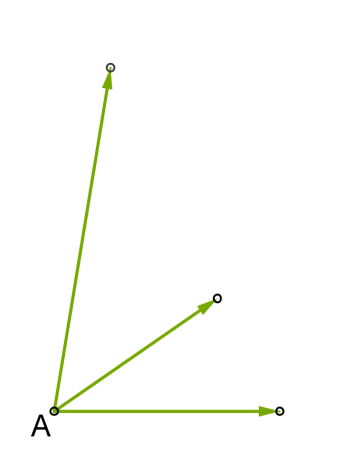
2. На цих трьох ребрах будують паралелепіпед;
3. Діагональ паралелепіпеда, яка виходить з цієї ж точки, зображує суми векторів , і
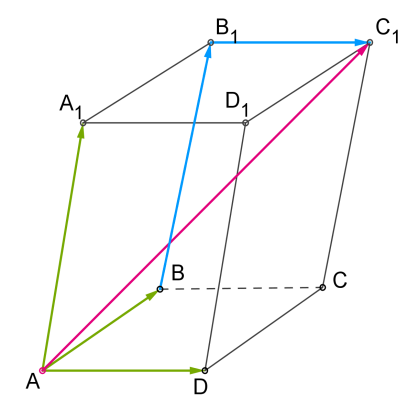
Розкладання вектора за трьома не компланарними векторами
Теорема про розкладання за базисом у просторі.
Будь-який вектор можна розкласти за трьома даними не компланарними векторами , і , при чому реальні коефіцієнти розкладання \(x\), \(y\) і \(z\) визначаються єдиним чином: .
Будь-який вектор можна розкласти за трьома даними не компланарними векторами , і , при чому реальні коефіцієнти розкладання \(x\), \(y\) і \(z\) визначаються єдиним чином: .