Основні поняття для векторів у просторі вводяться так само, як і для векторів на площині.
Вектором називається спрямований відрізок.
Будь-яка точка простору може розглядатися як нульовий вектор, початок і кінець якого збігаються. Нульовий вектор позначають .
Довжиною вектора називається довжина відповідного йому відрізка. Довжина нульового вектора дорівнює нулю.
.
Два ненульових вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Якщо ненульові вектори і колінеарні і промені \(AB\) і \(CD\) співнапрямлені, то і вектори називаються співнапрямленими. Якщо промені протилежні, то вектори називаються протилежно напрямленими.
Нульовий вектор співнапрямлений з будь-яким вектором.
Позначення: співнапрямлені вектори , протилежно напрямлені вектори .
Приклад:
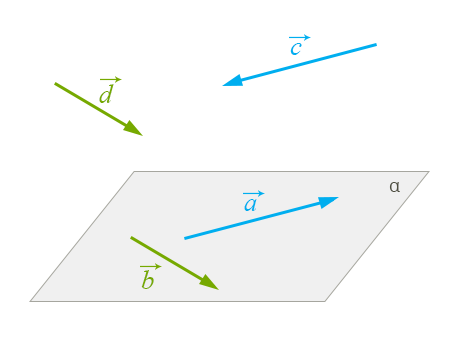
Вектори і , і попарно колінеарні. Причому, вектори і протилежно напрямлені, а вектори і - співнапрямлені.
Вектори називаються рівними, якщо вони співнапрямлені і рівні за довжиною.
Приклад:
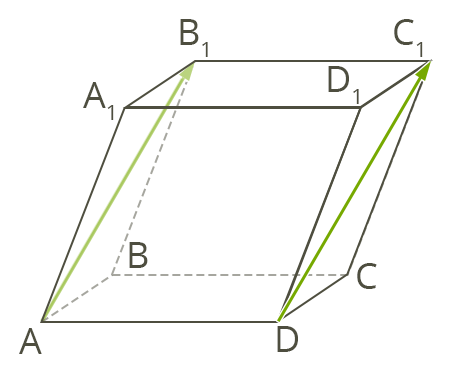
Приклад:
Вектори і рівні, оскільки і .
А вектори і — не рівні, тому що, незважаючи на рівність довжин, .
Якщо точка \(A\) — початок вектора, то кажуть, що заданий вектор відкладений від точки \(A\).
Від будь-якої точки можна відкласти вектор, рівний заданому, і притому тільки один.