Тетраедр. Види тетраедрів.
Тетраедр (чотиригранник) — багатогранник, гранями якого є чотири трикутники. (з грецької tetra — чотири та hedra — грань).

Рис. 1.
У тетраедра \(4\) грані, \(4\) вершини та \(6\) ребер (Рис.1.).
Один з трикутників називається основою тетраедра, а три інші — бічними гранями тетраедра.
Залежно від видів трикутників і їх розташування, виділяють різні види тетраедрів.
У шкільному курсі частіше говорять про наступні види тетраедра:
- рівногранний тетраедр
всі грані якого — рівні між собою трикутники;
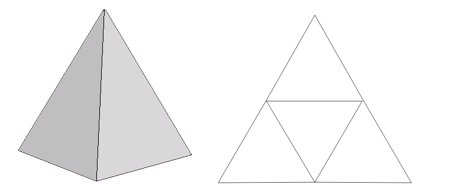
- правильная трикутна піраміда
основа — рівносторонній трикутник, усі бічні грані — рівнобедрені трикутники (Рис. 3.);
- правильний тетраедр
всі чотири грані якого — рівносторонні трикутники (Рис. 2.).


Рис. 2. Рис. 3.
Властивість правильного тетраедра:
З визначення правильного багатогранника виходить, що всі ребра тетраедра мають рівну довжину, а грані — рівну площу.
Паралелепіпед. Види паралелепіпедів.
Паралелепіпедом називається багатогранник, у якого \(6\) граней — паралелограми.
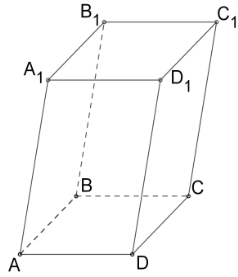
Рис. 4.
У паралелепіпеда \(6\) граней, \(8\) вершин і \(12\) ребер (Рис. 4.).
Дві грані паралелепіпеда, що мають спільне ребро, називаються суміжними, а не мають спільних ребер — протилежними.
Зазвичай виділяють якісь дві протилежні грані і називають їх основами, а інші грані — бічними гранями паралелепіпеда.
Ребра паралелепіпеда, що не належать основам, називають бічними ребрами.
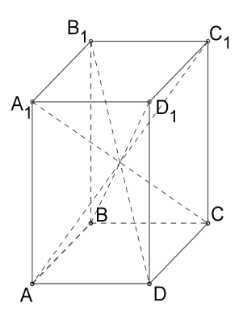
Рис. 5.
Залежно від видів паралелограмів і їх розташування, виділяють різні види паралелепіпедів:
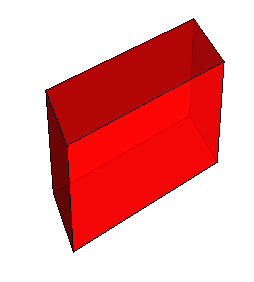
Паралелепіпеди можуть бути прямі і похилі.
У прямих паралелепіпедів бокові грані прямокутники (Рис. 5.),
у похилих — паралелограми (Рис. 4.).
Прямий паралелепіпед, у якого основа також прямокутник, називається прямокутним паралелепіпедом.
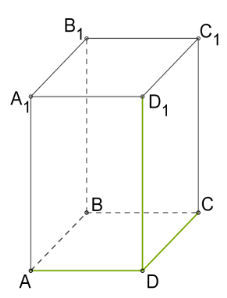
Рис. 6.
Довжина непаралельних ребер прямокутного паралелепіпеда називається його лінійними розмірами (вимірами).
У прямокутного паралелепіпеда три лінійні розміри , , (Рис. 6.).
Властивості паралелепіпеда:
— Протилежні грані паралелепіпеда рівні і паралельні.
— Протилежні грані паралелепіпеда рівні і паралельні.
— Усі чотири діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпіл.
— Бічні грані прямого паралелепіпеда — прямокутники.
Побудова перерізів тетраедра і паралелепіпеда.
Площиною перерізу багатогранника можна назвати будь-яку площину, що перетинає многогранник, по обидва боки якої знаходяться вершини багатогранника.
Січна площина перетинає грані багатогранників по відрізках.
Многокутник, сторонами якого є ці відрізки, називається перерізом багатогранника.
Так як у тетраедра \(4\) грані, то перерізом тетраедра може бути трикутник (Рис. 7.) або
чотирикутник (Рис. 8.).
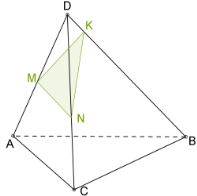
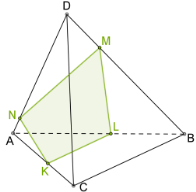
Рис. 7. Рис. 8.
У паралелепіпеда \(6\) граней, тому перерізом цього багатогранника може бути трикутник (Рис. 9.), чотирикутник (Рис. 10.), п’ятикутник (Рис. 11.) або шестикутник(Рис. 12.).
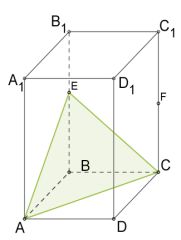 |
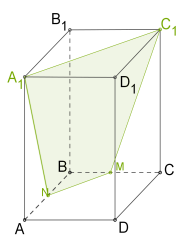 |
 |
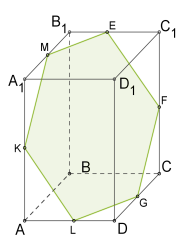 |
| Рис. 9. | Рис. 10. | Рис. 11. | Рис. 12. |
При побудові перерізу потрібно згадати наступні знання із попередніх тем:
1. Якщо дві точки прямої належать площині, то пряма лежить у цій площині.
2. Якщо дві площини мають спільну точку, то ці площини перетинаються по прямій, що містить дану точку.
3. Якщо площина перетинає дві паралельні площини, то прямі перетину паралельні.
Приклад:
Задача
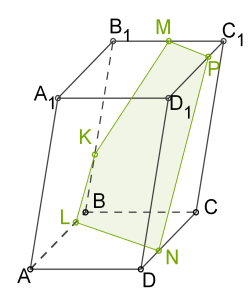
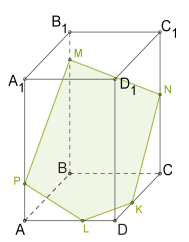
Побудувати переріз багатогранника площиною, яка проходить через точки \(K\), \(M\) і \(N\).
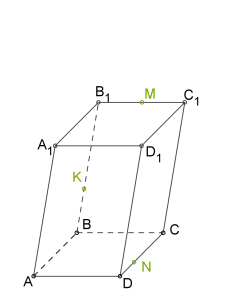
1. проведемо \(MK\) так як обидві точки лежать в одній площині
2. (непаралельні прямі в одній площині перетинаються)
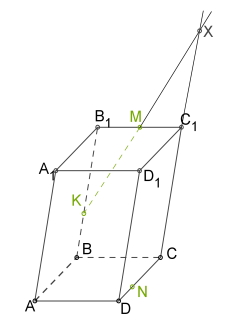
3. проведемо \(XN\) так як обидві точки лежать в одній площині
4.
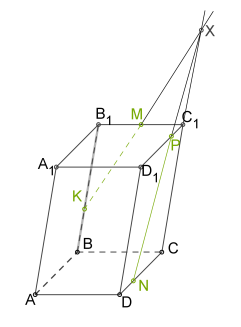
5. проведемо \(MP\) так як обидві точки лежать в одній площині
6. через точку \(N\) в площині основи так як прямі перетину паралельних площин з третьою площиною мають бути паралельні
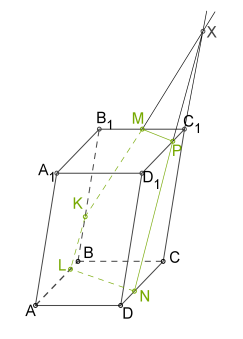
7. Сполучимо \(N\) і \(L\) і отримаємо переріз \(MPNLK\).