Взаємне розміщення прямих у просторі
Як відомо з курсу планіметрії, дві прямі в просторі можуть перетинатись (мають спільну точку) або бути паралельними (не мають спільних точок).
В просторі ми можемо уявити ситуацію, коли дві прямі не перетинаються і не є паралельними.
В просторі ми можемо уявити ситуацію, коли дві прямі не перетинаються і не є паралельними.

Одна дорога проходить під ескадою, а інша — над ескадою.

Кабелі мосту

Горизонтальні лінії даху і вертикальні лінії стін
Дві прямі називаються мимобіжними, якщо вони не лежать в одній площині.
Теорема «Ознака мимобіжних прямих»
Якщо одна із двох прямих лежить в деякій площині, а інша пряма перетинає цю площину в точці, що не лежить на першій прямій, то ці прямі мимобіжні (не лежать в одній площині).
Розглянемо пряму \(AB\), що лежить в площині і пряму \(CD\), яка перетинає площину в точці \(D\), яка не лежить на прямій \(AB\).
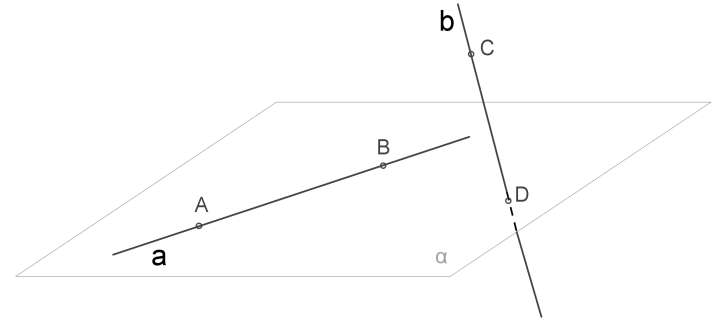
1. Припустимо, що прямі \(AB\) і \(CD\) лежать в одній площині.
2. Це означає, що площина проходить через пряму \(AB\) і точку \(D\), тобто вона співпадає з площиною \(α\).
3. Маємо протиріччя умові теореми, отже пряма \(CD\) не лежить в площині \(α\), а перетинає її.
Теорема доведена.
2. Це означає, що площина проходить через пряму \(AB\) і точку \(D\), тобто вона співпадає з площиною \(α\).
3. Маємо протиріччя умові теореми, отже пряма \(CD\) не лежить в площині \(α\), а перетинає її.
Теорема доведена.
В просторі прямі розміщені наступним чином:
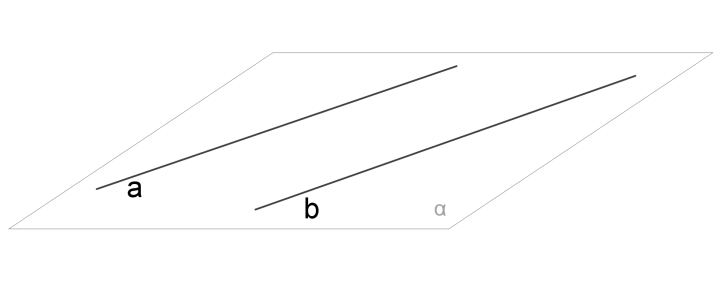
1. Паралельні
1. Паралельні
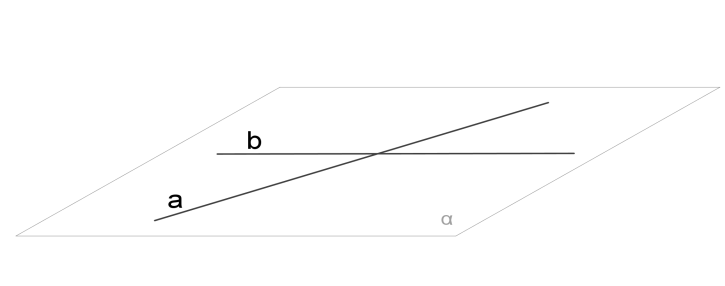
2. Перетинаються
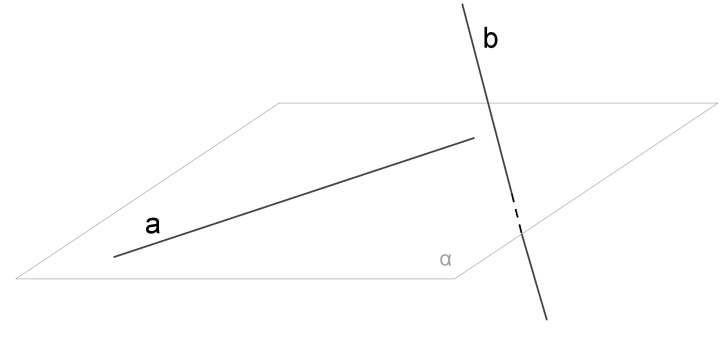
3. Мимобіжні
Теорема
Через кожну з двох мимобіжних прямих проходить площина, паралельна іншій прямій, і лише одна.
Доведення
Розглянемо мимобіжні прямі \(AB\) і \(CD\).
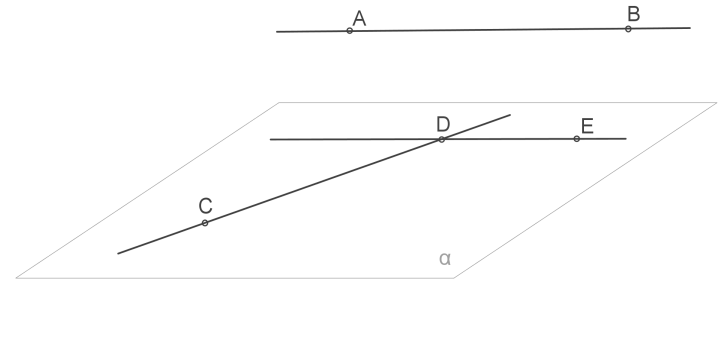

1. Через точку \(D\) можно провести пряму \(DE\) паралельну \(AB\).
2. Через прямі, що перетинаються \(CD\) і \(DE\) можно провести площину \(α\)
3. Так як пряма \(АB\) не лежить в цій площині і паралельна прямій \(DE\), то вона паралельна площині.
2. Через прямі, що перетинаються \(CD\) і \(DE\) можно провести площину \(α\)
3. Так як пряма \(АB\) не лежить в цій площині і паралельна прямій \(DE\), то вона паралельна площині.
4. Ця площина єдина, оскільки будь-яка інша площина, що проходить через \(CD\), буде перетинатись з \(DE\) і \(AB\).
Теорема доведена.
Теорема доведена.
Кути між прямими
2. Кутом між двома прямими, що перетинаються, називають величину меншого з кутів, утворених цими прямими. Якщо всі кути рівні, то ці прямі перпендикулярні (утворюють кут ).
3. Кутом між двома мимобіжними прямими називають кут між двома прямими, що перетинаються, відповідно паралельними мимобіжним прямим.
Зверни увагу!
Провести відповідні паралельні прямі до даних мимобіжних прямих можна через будь-яку точку. Іноді зручно вибрати цю точку на одній з даних мимобіжних прямих і провести через цю точку пряму, паралельну другій мимобіжній прямій.
Приклад:
Дано куб
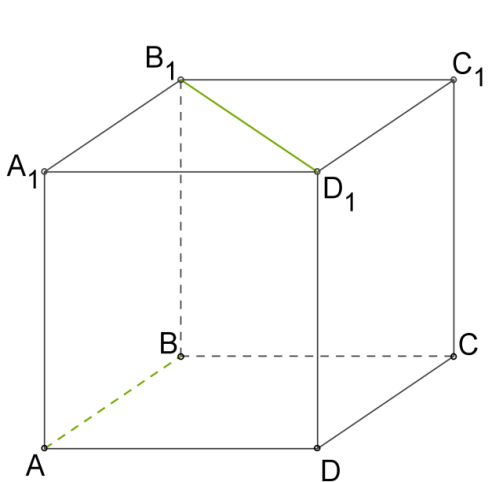
Знайти кут між і
Виберемо точку на прямій і проведемо через пряму паралельно
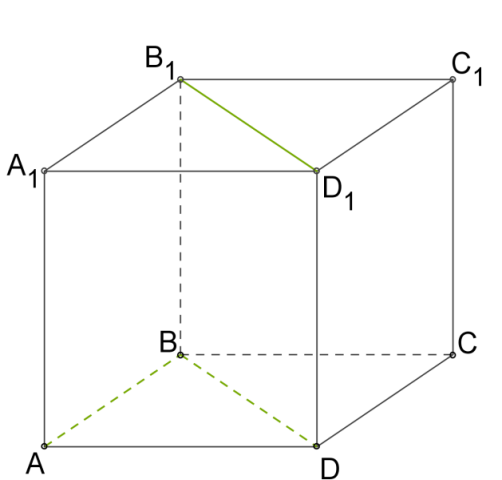
Кут між і так як квадрат.
Відповідно кут між і також .