
Двогранний кут — це частина простору, розташована між двома півплощинами, що мають одну загальну межу.

Якщо в просторі перетинаються дві площини, виходять чотири двогранних кути (аналогічно як при перетині двох прямих виходять чотири кути). Розглянемо один з них.

Півплощини і , що утворюють двогранний кут, називаються його гранями.
Спільна пряма \(a\) цих граней називається ребром двогранного кута.
Спільна пряма \(a\) цих граней називається ребром двогранного кута.
Позначимо на ребрі \(a\) двогранного кута довільну точку \(С\) і проведемо дві прямі, що перетинаються і , а через ці прямі площину перпендикулярно ребру \(a\).
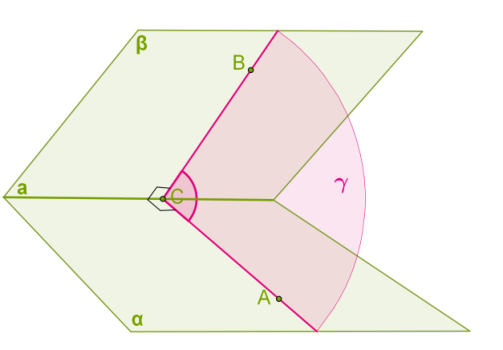
Лінії перетину \(AC\) і \(BC\) півплощин і з площиною утворюють деякий кут . Цей кут називається лінійним кутом двогранного кута. Величина лінійного кута не залежить від вибору точки \(C\) на ребрі \(a\) .
Зверни увагу!
Величина двогранного кута \(0° <\) \(< 180°\).
Якщо площини паралельні, то кут між ними дорівнює \(0 °\) за визначенням.
Якщо при перетині площин один з двогранних кутів \(90 °\), то три інші кути теж \(90 °\). Ці площини називають перпендикулярними.
Якщо при перетині площин один з двогранних кутів \(90 °\), то три інші кути теж \(90 °\). Ці площини називають перпендикулярними.
Наступні теореми, які тут наведемо без доведення, можуть знадобиться при розв'язанні задач.
1. Якщо одна з двох площин проходить через пряму перпендикулярну до іншої площини, то такі площини перпендикулярні.
2. Площина, перпендикулярна прямій, на якій перетинаються дві площини, перпендикулярна кожній з цих площин.
3. Якщо дві площини перпендикулярні і в одній з них проведена пряма перпендикулярно лінії перетину площин, то ця пряма перпендикулярна другій площині.
Багатогранні кути.
Пояснимо поняття багатогранних кутів.
Уявімо кілька променів у просторі із загальним початком. Їх можна представити теж як частину ліній перетину площин — трьох, чотирьох або більше і назвати ребрами багатогранного кута.
Уявімо кілька променів у просторі із загальним початком. Їх можна представити теж як частину ліній перетину площин — трьох, чотирьох або більше і назвати ребрами багатогранного кута.
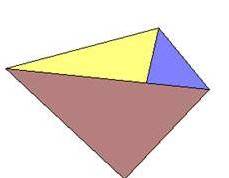 Тригранний кут
Тригранний кут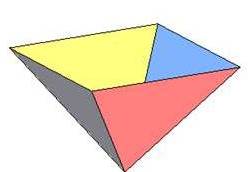 Чотиригранний кут
Чотиригранний кут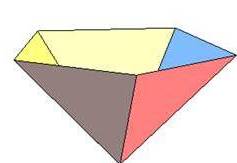 П'ятигранний кут
П'ятигранний кутКожні два промені утворюють кут, який називають плоским кутом багатогранного кута.
Зверни увагу!
Кожен плоский кут тригранного кута менше суми двох інших плоских кутів.
Сума плоских кутів багатогранного кута менше \(360°\).