Багатогранник, одна грань якого є \(n\) — кутником, а інші грані — трикутники із загальною вершиною, називається пірамідою, \(n\)-кутник називається основою піраміди, а трикутники — бічними гранями.
Спільна вершина бічних граней називається вершиною піраміди.
Відрізки, що з'єднують вершину піраміди з вершинами основи, називаються ребрами піраміди.
Відрізки, що з'єднують вершину піраміди з вершинами основи, називаються ребрами піраміди.
Залежно від кількості сторін основи, піраміди можуть бути трикутними, чотирикутними, п'ятикутними і т. д.
Перпендикуляр, проведений з вершини піраміди до площини основи, називається висотою піраміди.
Щоб намалювати піраміду, потрібно дотримуватися певного порядку:
1. першим малюється основа,
2. за умовою завдання знаходиться проекція вершини на площині основи,
3. вертикально проводиться висота,
4. проводяться ребра.
2. за умовою завдання знаходиться проекція вершини на площині основи,
3. вертикально проводиться висота,
4. проводяться ребра.
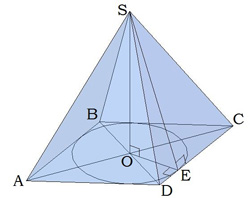
На малюнку зображена чотирикутна піраміда \(SABCD\)
(першою пишуть букву вершини).
(першою пишуть букву вершини).
Основа — чотирикутник \(ABCD\).
Вершина проектується в точку перетину діагоналей \(O\) — основа висоти або проекція вершини.
\(SA\), \(SB\), \(SC\), \(SD\) — ребра піраміди,
\(AB\), \(BC\), \(CD\), \(DA\) — сторони основи.
В курсі середньої школи в основному є завдання, в яких надані:
- правильна піраміда (вершина проектується в центр основи);
- піраміда, вершина якої проектується в центр описаного кола;
- піраміда, вершина якої проектується в центр вписаного кола;
- піраміда, висота якої співпадає з боковим ребром;
- піраміда, висота якої також є висотою бічної грані.
- піраміда, вершина якої проектується в центр описаного кола;
- піраміда, вершина якої проектується в центр вписаного кола;
- піраміда, висота якої співпадає з боковим ребром;
- піраміда, висота якої також є висотою бічної грані.
Кути піраміди
Кути, які утворені бічною гранню і основою піраміди, називаються двогранними кутами при основі піраміди.
Щоб визначити цей кут, часто потрібно використовувати теорему про три перпендикуляри.
Кути, які утворені бічним ребром і його проекцією на площину основи, називаються кутами між бічним ребром і площиною основи.
Кут, який утворений двома бічними гранями, називається двогранним кутом при бічному ребрі піраміди.
Кут, який утворений двома бічними ребрами однієї грані піраміди, називається кутом при вершині піраміди.
Кут, який утворений двома бічними ребрами однієї грані піраміди, називається кутом при вершині піраміди.
На малюнку \(DSC\).
Основні формули піраміди
Площа бічної поверхні дорівнює сумі площ всіх бічних граней піраміди:
Деякі формули підійдуть лише для певних видів піраміди.
Площа повної поверхні
Об'єм піраміди \(V =\) \(H\), де \(H\) — висота піраміди.
Формула об'єму використовується для пірамід будь-якого виду.
