Конус — тіло обертання, утворене в результаті обертання прямокутного трикутника навколо його катета.
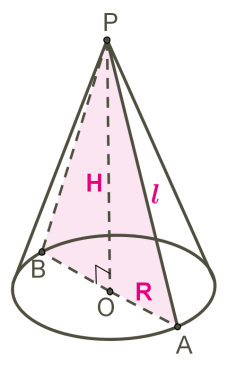
Трикутник \(POA\) обертається навколо сторони \(PO\).
\(PO\) — вісь конуса і висота конуса.
\(P\) — вершина конуса.
\(PA\) — твірна конуса.
Коло з центром \(O\) — основа конуса.
\(AO\) — радіус основи конуса.
Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь \(PO\) конуса.
Осьовий переріз конуса — це трикутник.
\(APB\) — осьовий переріз конуса.
\(PO\) — вісь конуса і висота конуса.
\(P\) — вершина конуса.
\(PA\) — твірна конуса.
Коло з центром \(O\) — основа конуса.
\(AO\) — радіус основи конуса.
Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь \(PO\) конуса.
Осьовий переріз конуса — це трикутник.
\(APB\) — осьовий переріз конуса.
— кути між твірними і основою конуса.
Розгорткою бічної поверхні конуса є круговий сектор. Довжина дуги сектора — це довжина кола основи конуса довжиною , кут розгортки бічної поверхні .
У конусі не можна позначити кут розгортки.
На розгортці конуса не можна позначити висоту й радіус конуса.
На розгортці конуса не можна позначити висоту й радіус конуса.
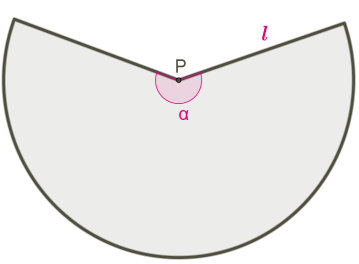
Радіус сектора — це твірна конуса.
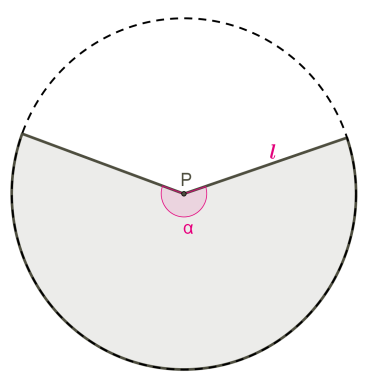
Таким чином, бічна поверхня конуса є частиною повного кола з радіусом \(l\):
Довжина дуги також є частиною довжини повного кола з радіусом \(l\), але в той же час довжина дуги — це довжина кола основи конуса з радіусом \(R\).
Порівняємо вирази довжини дуги й виразимо через \(R\):
Порівняємо вирази довжини дуги й виразимо через \(R\):
Отримуємо ще одну формулу бічної поверхні конуса, не використовується кут розгортки бічної поверхні:
Зрізаний конус
Якщо провести переріз конуса площиною, перпендикулярною осі конуса, тоді ця площина розбиває конус на дві частини, одна з яких — конус, а іншу частину називають зрізаним конусом.
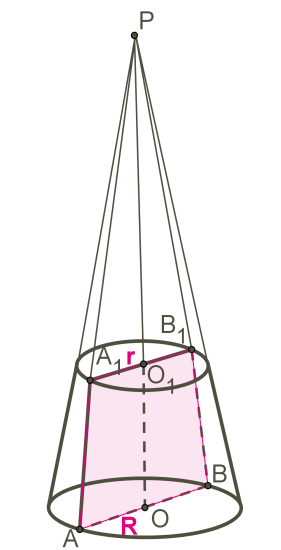
Також зрізаний конус можна розглядати, як тіло обертання, яке утворилося в результаті обертання прямокутної трапеції навколо бічної сторони (яка перпендикулярна до основи трапеції) або в результаті обертання рівнобедреної трапеції навколо висоти, проведеної через серединні точки основ трапеції.
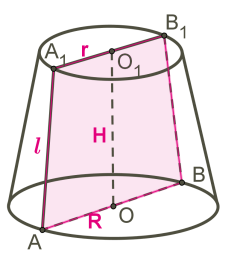
— вісь конуса і висота конуса.
— твірна конуса.
Кола з центрами \(O\) і — основи зрізаного конуса.
\(AO\) і — радіуси основ конуса.
Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь конуса.
Осьовий переріз конуса — це рівнобедрена трапеція.
— осьовий переріз конуса.
Бічна поверхня визначається, як різниця бічної поверхні даного конуса і відтятого конуса:
Оскільки , тоді сторони їх пропорційні:
Таким чином, отримуємо формулу бічної поверхні зрізаного конуса, яка містить радіуси основ і твірну зрізаного конуса: