Опуклий многогранник називається правильним, якщо:
1. усі його грані - рівні правильні многокутники;
2. у кожній його вершині сходиться одне і те ж число ребер.
1. усі його грані - рівні правильні многокутники;
2. у кожній його вершині сходиться одне і те ж число ребер.
Всі ребра правильного многогранника рівні, а також рівні всі двогранні кути, що містять дві грані зі спільним ребром.
1. Які правильні многокутники можуть бути гранями правильного многогранника?
2. Скільки граней може мати правильний многогранник?
Не існує правильного многогранника, гранями якого є правильні многокутники, якщо число їх сторін \(6\) або більше, тобто правильні \(n\)-кутники, якщо .
2. У кожній вершині многогранника повинно бути не менше трьох кутів.
3. Навіть при трьох кутах сума всіх кутів вже досягає .
4. Сума всіх плоских кутів при кожній вершині опуклого многогранника менше .
Отже, не існує правильного многогранника, гранями якого були б правильні \(n\)-кутники, якщо .
Тільки правильні трикутники, чотирикутники (квадрати) і п'ятикутники можуть бути гранями правильного многогранника.
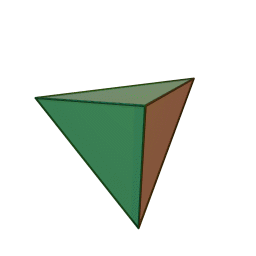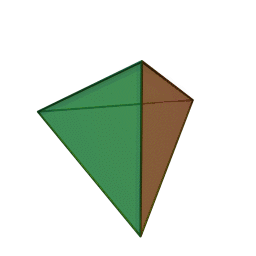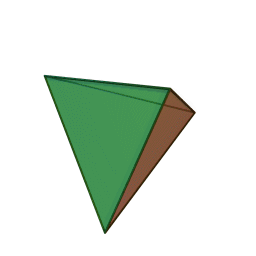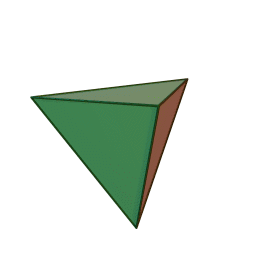
Чи існують правильні многогранники з такими гранями і скільки граней вони мають? Найменше можливе число граней — чотири.
Теорема Ейлера і правильні многогранники
Теорема Ейлера.
У будь-якому опуклому многограннику сума числа граней і числа вершин на \(2\) більше числа ребер.
За допомогою теореми Ейлера ми можемо отримати відповідь на питання:
які правильні многогранники можуть існувати?
які правильні многогранники можуть існувати?
1. Нехай кількість ребер правильного многогранника, що виходять з однієї вершини, дорівнює \(m\), а гранями є правильні \(n\) — кутники.
2. Позначимо величини, що входять у формулу Ейлера \(В\) (вершини) і \(Г\) (грані) через:
\(Р\) (ребра), \(m\), \(n\), де \(n\) і \(m\) — цілі числа і \(m ≥ 3\), \(n =\) \(3;\) \(4\) \(або\) \(5\).
3. Оскільки кожне ребро з'єднує дві вершини, і в кожній вершині сходяться \(m\) ребер, тоді \(2Р=Вm\).
Тоді
4. Оскільки кожне ребро многогранника міститься у двох гранях, тоді \(Гn = 2Р\).
Тоді
5. Підставляючи отримані вирази для \(Г\) і \(В\) у формулу Ейлера \(Г + В - Р = 2\), отримуємо
6. Поділивши обидві частини рівності на \(2Р\), отримаємо
7. Розв'яжемо це рівняння при \(n =\) \(3\) і знайдемо допустимі значення \(m\).
За змістом \(Р > 0\), отже \(3 ≤ m ≤5\).
Таким чином теорема Ейлера дозволяє існування наступних правильних многогранників:
1. \(m=3, n=3, P=6, Г=4\) — тетраедр
2. \(m=3, n=4, P=12, Г=6\) — куб
3. \(m=3, n=5, P=30, Г=12\) — додекаедр
4. \(m=4, n=3, P=12, Г=8\) — октаедр
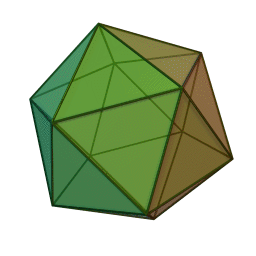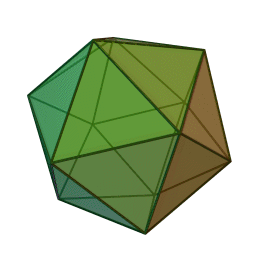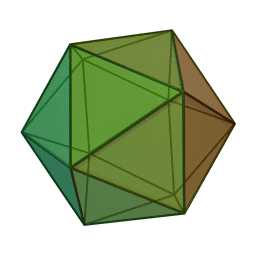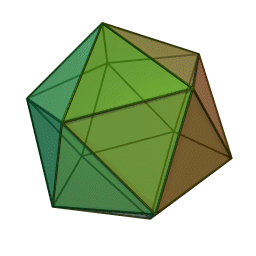
5. \(m=5, n=3, P=30, Г=20\) — ікосаедр
4. \(m=4, n=3, P=12, Г=8\) — октаедр
5. \(m=5, n=3, P=30, Г=20\) — ікосаедр
Доведено існування правильних многогранників:
тетраедр із \(4\) гранями, \(6\) ребрами і \(4\) вершинами:
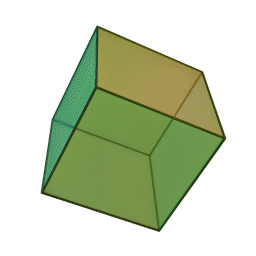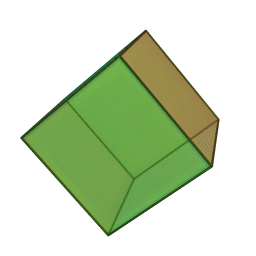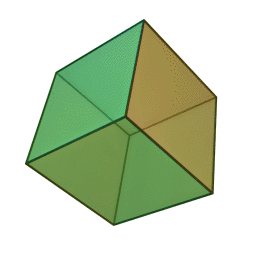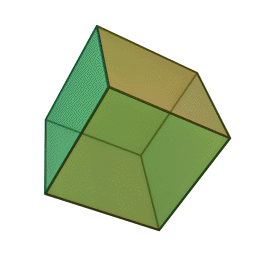
куб із \(6\) гранями, \(12\) ребрами і \(8\) вершинами:
октаедр із \(8\) гранями, \(12\) ребрами і \(6\) вершинами:
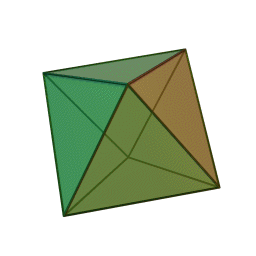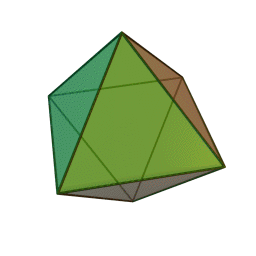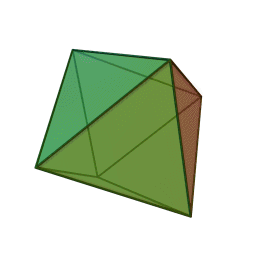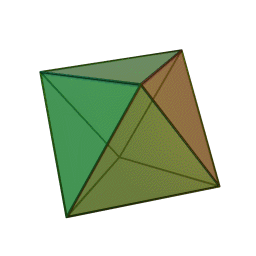
додекаедр із \(12\) гранями, \(30\) ребрами і \(20\) вершинами:
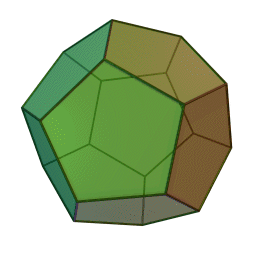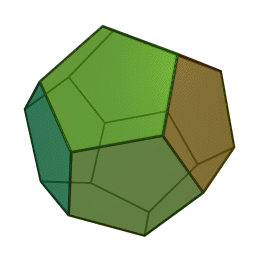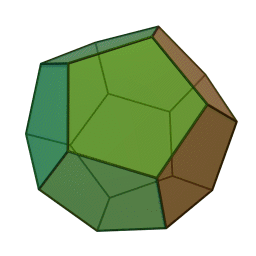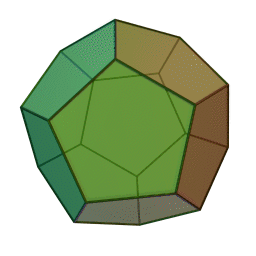
ікосаедр із \(20\) гранями, \(30\) ребрами і \(12\) вершинами: