Циліндр називається описаним навколо призми, якщо багатокутники основ призми вписані в кола основ циліндра, а твірні циліндра є бічними ребрами призми.
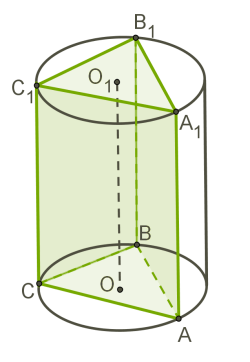
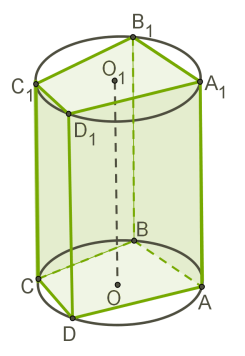
Циліндр можна описати лише навколо такої прямої призми, навколо основи якої можна описати коло..
Наприклад, циліндр завжди можна описати навколо прямої трикутної призми, навколо правильної призми.
Малюнок складається залежно від змісту завдання, часто досить малюнка основи комбінацій цих тіл, оскільки висота призми дорівнює висоті циліндра.
Малюнок складається залежно від змісту завдання, часто досить малюнка основи комбінацій цих тіл, оскільки висота призми дорівнює висоті циліндра.
Коло основи циліндра описано навколо багатокутника основи призми.
Радіус циліндра — це радіус кола, описаного навколо багатокутника основи призми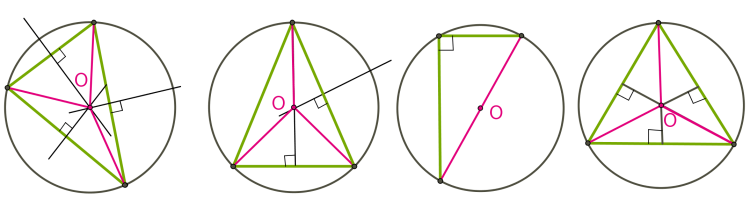
Радіус циліндра — це радіус кола, описаного навколо багатокутника основи призми
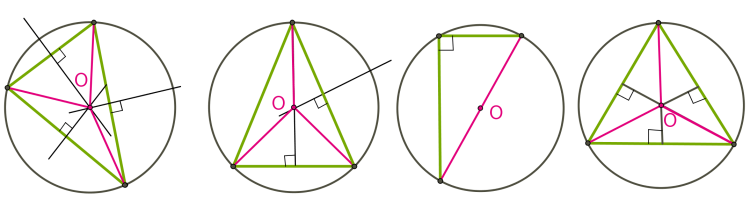
Центр коло, описаного навколо трикутника, є точкою перетину серединних перпендикулярів до сторін трикутника.
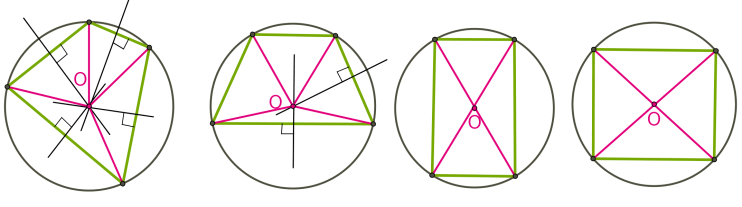
Центр кола, описаного навколо чотирикутника, є точкою перетину серединних перпендикулярів до сторін чотирикутника. Навколо чотирикутника можна описати коло, якщо суми протилежних кутів дорівнюють .
Формули обчислення радіуса \(R\) описаного кола
| Правильний трикутник | \(R =\) \(R=\) |
| Прямокутний трикутник | \(R=\) гіпотенузи |
| Довільний трикутник | |
| Квадрат | \(R =\) |
| Прямокутник | \(R =\) |
| Правильний шестикутник | \(R = a\) |
Циліндр вписаний у призму, якщо кола основ циліндра вписані у багатокутники основ призми.
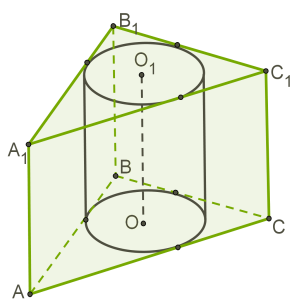
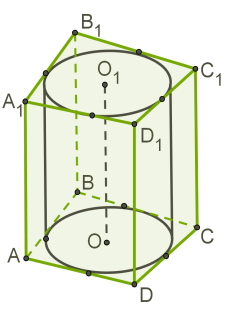
Циліндр можна вписати тільки у таку пряму призму, у багатокутник основи якої, можна вписати коло.
Наприклад, циліндр завжди можна вписати у пряму трикутну призму, у правильну призму.
Малюнок створюється в залежності від змісту завдання, часто досить намалювати основу комбінацій цих тіл, оскільки висота циліндра дорівнює висоті призми.
Малюнок створюється в залежності від змісту завдання, часто досить намалювати основу комбінацій цих тіл, оскільки висота циліндра дорівнює висоті призми.
Коло основи циліндра вписане у багатокутник основи призми.
Радіус циліндра — радіус кола, вписаного у багатокутник основи призми.
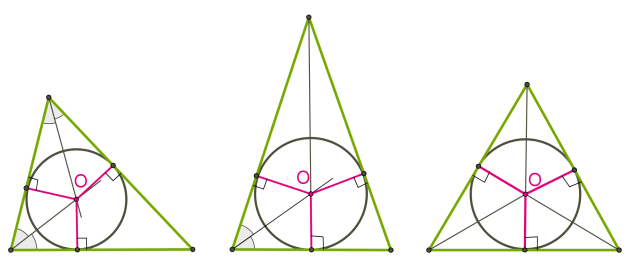
Центр вписаного у трикутник кола знаходиться у точці перетину бісектрис трикутника.
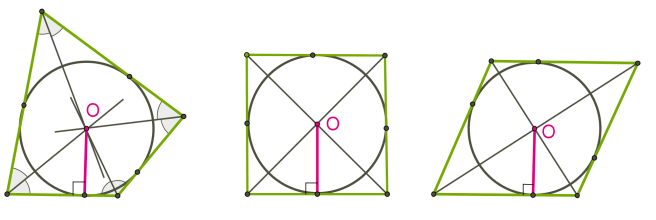
Центр кола, вписаного у чотирикутник, знаходиться у точці перетину бісектрис чотирикутника. В чотирикутник можна вписати коло, якщо суми довжин протилежних сторін рівні.
Формули обчислення радіуса \ (r \) вписаного кола
| Правильний трикутник | |
| Довільний (і прямокутний) трикутник | \(r =\) |
| Квадрат | \(r =\) \(a\) |
| Ромб | \(r =\) або \(r =\) від \(h\) |
| Правильний шестикутник | \(r =\) |