На площині пряма і коло можуть перетинатися або не перетинатися. При перетині вони можуть мати одну або дві спільні точки.
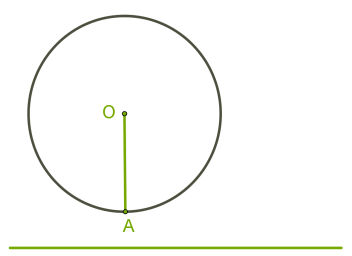
\(1.\) Якщо відстань від центра кола до прямої більша від радіуса, то в прямої і кола немає спільних точок.
\(2.\) Якщо відстань від центра кола до прямої менша від радіуса, то в прямої і кола дві спільні точки.
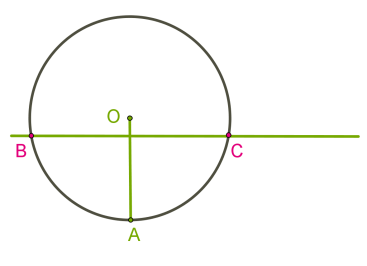
У цьому випадку пряму називають січною кола.
Якщо пряма має дві спільні точки з колом, то вона називається січною.
\(3.\) Якщо відстань від центра кола до прямої дорівнює радіусу, то в прямої і кола одна спільна точка.
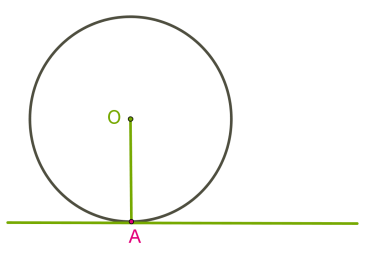
У цьому випадку пряму називають дотичною до кола.
Дотичною до кола називається пряма, що має з колом одну спільну точку.
Дотична до кола перпендикулярна радіусу, проведеному до точки дотику.
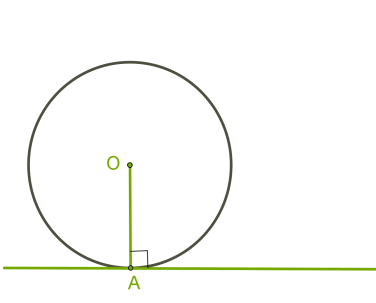
Припустимо, що радіус \(OA\) не перпендикулярний до прямої, але є похилим. Тоді з точки \(O\) можна провести перпендикуляр до прямої, який буде коротшим, ніж радіус.
Це означає, що відстань від центра кола до прямої менша від радіуса, і в прямої та кола повинні бути дві спільні точки. Але це суперечить умові, тож наше припущення неправильне.
Якщо з точки до кола проведено дві дотичні, то:
\(a)\) довжини відрізків дотичних від цієї точки до точки дотику рівні;
\(b)\) пряма, що проходить через центр кола і цю точку, ділить кут між дотичними навпіл.
\(a)\) довжини відрізків дотичних від цієї точки до точки дотику рівні;
\(b)\) пряма, що проходить через центр кола і цю точку, ділить кут між дотичними навпіл.
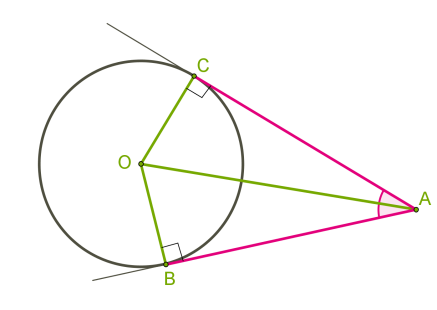
Нехай \(AB\) та \(AC\) — дотичні до кола з центром \(O.\) Потрібно довести, що \(AB = AC\) та \(OA\) є бісектрисою кута \(A.\)
Трикутники \(OBA\) та \(OCA\) — прямокутні, оскільки дотичні перпендикулярні до радіусів кола у точках \(B\) та \(C.\) Сторона \(OA\) — спільна. Катети \(OB\) та \(OC\) рівні як радіуси одного й того самого кола. Трикутники рівні за гіпотенузою та катетом, звідси рівні й катети \(AB\) та \(AC\), а також кути \(BAO\) і \(CAO\), тобто \(OA\) ділить кут навпіл.
