Основні задачі на побудову за допомогою циркуля та лінійки

Мета розв’язування задач на побудову — це побудова геометричних фігур із заданими властивостями за допомогою креслярських інструментів: циркуля й лінійки без вимірювальних поділок.
За допомогою лінійки можна провести:
- довільну пряму;
- пряму, що проходить через дану точку;
- пряму, що проходить через дві дані точки.
Зверни увагу!
Ніяких інших побудов лінійкою виконувати не можна, тобто, за допомогою лінійки не можна відкладати відрізки заданої довжини.
За допомогою циркуля можна:
- провести коло (частину кола) довільного або заданого радіуса з довільним або заданим центром;
- відкласти від початку даного променя відрізок заданої довжини.
Перелічені операції називають елементарними побудовами.
Розв’язати задачу на побудову — означає:
- знайти послідовність елементарних побудов, після виконання яких шукана фігура вважається побудованою;
- довести, що саме ця фігура задовольняє умову задачі.
Розглянемо п'ять основних геометричних побудов, у яких використовуємо згадані дії (побудова прямої та кола):
\(1.\) Побудова відрізка, що дорівнює даному.
\(2.\) Побудова кута, що дорівнює даному.
\(3.\) Побудова бісектриси кута.
\(4.\) Побудова перпендикулярних прямих.
\(5.\) Побудова середини відрізка.
\(2.\) Побудова кута, що дорівнює даному.
\(3.\) Побудова бісектриси кута.
\(4.\) Побудова перпендикулярних прямих.
\(5.\) Побудова середини відрізка.
\(1.\) Побудова відрізка, що дорівнює даному
Див. відео.
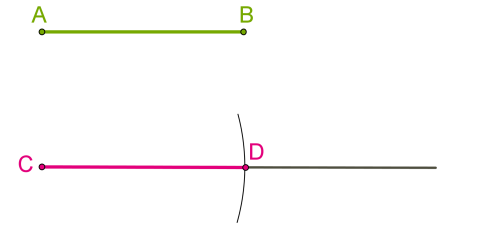
Зрозуміло, що таким чином ми отримали відрізок, який дорівнює даному. Відповідно до означення кола, він складається з точок, розташованих на рівній відстані (радіусі) від певної точки (центр кола).
Якщо центром є початкова точка променя \(C,\) радіусом — даний відрізок \(AB,\) то точка перетину кола і променя \(D\) і є шуканою кінцевою точкою відрізка \(CD,\) що дорівнює даному відрізку \(AB.\)
\(2.\) Побудова кута, що дорівнює даному
Див. відео.
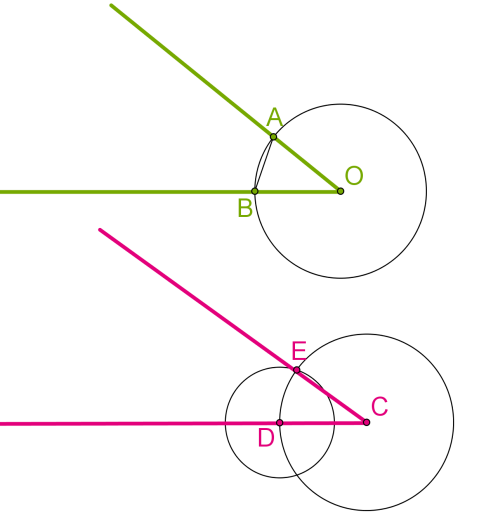
Доведемо, що побудований кут \(ECD\) і є той шуканий кут, що дорівнює даному куту \(AOB.\)
Якщо ми побудували коло з центром \(C\) (початковою точкою променя) і таким самим радіусом, як у кола з центром \(O,\) то \(CD\) \(=\) \(OB.\)
Якщо далі ми побудували коло з центром \(D\) і радісуом, рівним відрізку \(BA,\) і отримали точку перетину обох кіл \(E,\) то \(BA\) \(=\) \(DE.\)
Ми провели промінь \(CE.\) Очевидно, що \(OA\) \(=\) \(CE.\)
Отже, трикутники \(AOB\) і \(ECD\) рівні за третьою ознакою рівності трикутників. У рівних трикутників відповідні елементи рівні, зокрема кут \(ECD\) дорівнює куту \(AOB.\)
\(3.\) Побудова бісектриси кута
Див. відео.
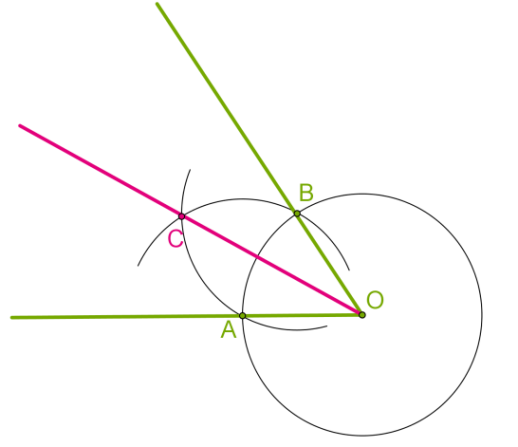
Щоб довести, що \(OC\) дійсно ділить кут \(AOB\) навпіл, достатньо розглянути трикутники \(AOC\) і \(BOC.\)
\(OA = OB\) як радіуси одного кола, а \(AC = BC,\) оскільки при побудові ми вибрали однакові радіуси для обох кіл.
Сторона \(OC\) — спільна.
Ці трикутники рівні за третьою ознакою рівності трикутників, тож їх відповідні кути рівні.
Отже, \(AOC\) і \(BOC\) — дві рівні частини одного кута, і це означає, що промінь \(OC\) ділить кут навпіл.
\(4.\) Побудова перпендикулярних прямих
Див. відео.
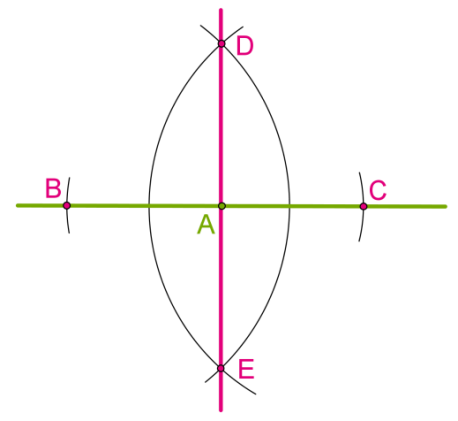
Чому \(DE\) є перпендикулярною до \(BC?\)
\(AB = AC,\) оскільки ці точки були відкладені при побудові.
\(BD = CD,\) оскільки обидва кола побудували з однаковими радіусами.
Отже, \(DA\) або \(EA\) — медіани до основи рівнобедрених трикутників \(ADB\) або \(AEB.\)
Медіана в трикутнику є також висотою, тобто перпендикулярна до основи.
\(5.\) Побудова середини відрізка
Див. відео.
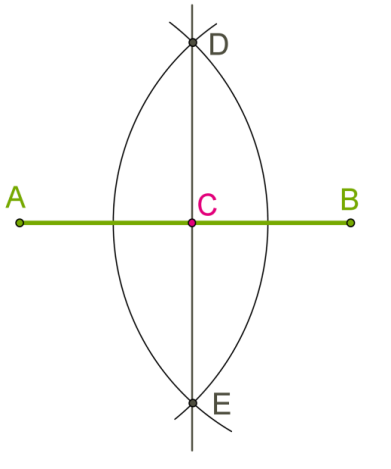
Ця побудова така ж, як у випадку побудови перпендикулярних прямих, і вже доведено, що \(DC\) або \(EC\) ділить \(AB\) навпіл, тобто \(C\) — середина відрізка \(AB.\)
