Друга ознака рівності трикутників
Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.
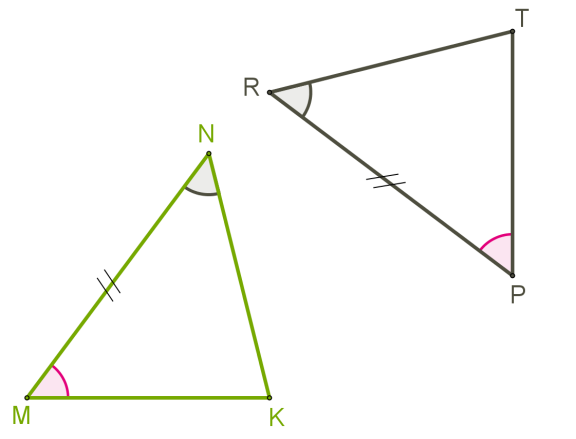
Як і при доведенні першої ознаки, потрібно переконатися, чи достатньо цих даних для рівності трикутників. Чи можна накласти трикутники один на одний?
\(1.\) Оскільки \(,\) то ці відрізки накладаються, якщо поєднати їхні кінцеві точки.
\(2.\) Оскільки і \(,\) то промені \(MK\) і \(NK\) накладуться відповідно на промені \(PT\) і \(RT.\)
\(3.\) Якщо збігаються промені, то збігаються точки їх перетину \(K\) і \(T.\)
\(4.\) Поєднано всі вершини трикутників, тобто і повністю накладаються. Отже, трикутники рівні.
