Ознаки, які ми розглядали раніше, і властивості, які будемо розглядати далі, доводяться різними способами.
Ознака — це певний факт, завдяки якому ми встановлюємо правильність поданого судження про певний об'єкт.
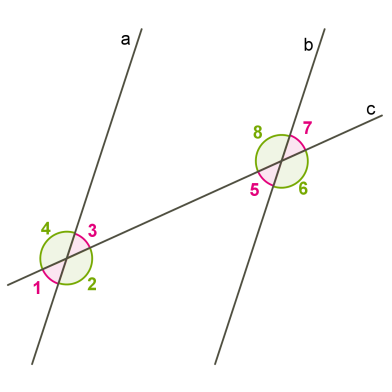
Якщо при перетині двох прямих третьою (січною), внутрішні різносторонні кути рівні, то ці дві прямі паралельні.
Якщо ми впевнені у правильності судження, ми формулюємо властивість об'єкта.
Якщо дві прямі паралельні, то при перетині їх третьою січною різносторонні кути є рівними.
Аксіома — це істина, яку не потрібно доводити. У кожній науці є свої аксіоми, на основі яких будуються всі подальші твердження та доведення.
Аксіома паралельності прямих
На одній площині із заданою прямою через точку, що не лежить на цій прямій, можна провести лише одну пряму, паралельну даній прямій.
Іноді вищезгадану аксіому вважають однією із властивостей паралельних прямих, але на правильності цієї аксіоми будується багато доведень у геометрії.
Інші властивості паралельних прямих
\(1.\) Якщо одна з пари паралельних прямих паралельна третій прямій, то й друга пряма паралельна третій прямій.
\(2.\) Якщо певна пряма перетинає одну з двох паралельних прямих, то вона перетинає й другу паралельну пряму.
Ці властивості, на відміну від аксіоми, потрібно довести.
Доведення першої властивості.
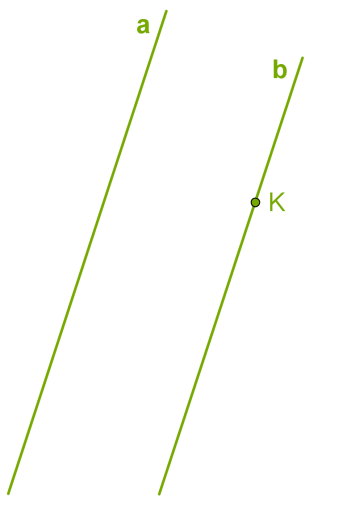
Маємо дві паралельні прямі \(a\) і \(b.\) Чи правильне твердження, що якщо пряма \(c\) паралельна прямій \(a,\) то вона паралельна і прямій \(b?\)
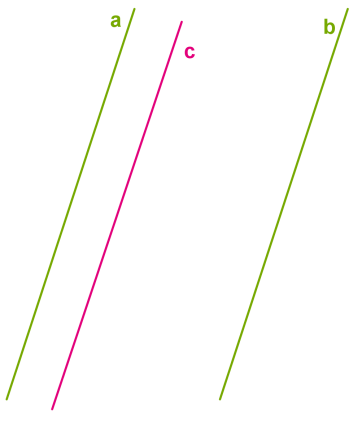
Скористаємося протилежним твердженням.
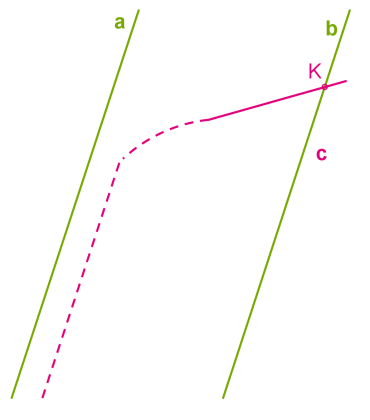
Припустимо, що можлива ситуація, коли пряма \(c\) паралельна одній із паралельних прямих — прямій \(a,\) і перетинає іншу пряму \(b\) у певній точці \(K.\)
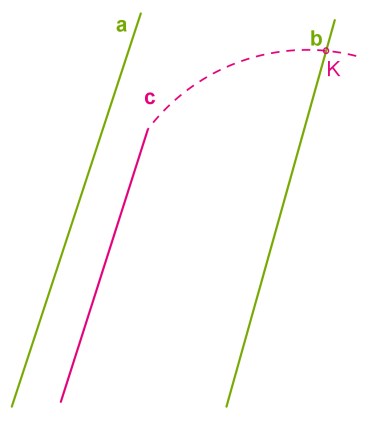
Виникає суперечність із аксіомою паралельних прямих. Ми маємо ситуацію, коли через точку проходять дві прямі, які перетинаються і паралельні одній і тій самій прямій \(a.\) Так не може бути, отже, прямі \(b\) і \(c\) перетинатися не можуть.
Ми довели правильність твердження. Якщо одна з пари паралельних прямих паралельна третій прямій, то й друга пряма паралельна третій.
Спробуй довести самостійно другу властивість.
Якщо певна пряма \(c\) перетинає одну з двох паралельних прямих \(a,\) то вона перетинає і другу паралельну пряму \(b.\)
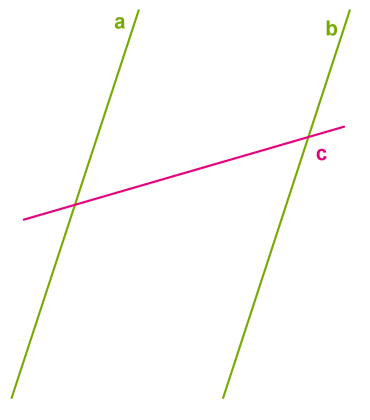
Таким самим методом від протилежного твердження спробуй уявити, що можлива ситуація, коли пряма перетинає одну з паралельних прямих, але не перетинає іншу.
Властивості кутів, які утворюються при перетині двох паралельних прямих із третьою (січною), ми вже назвали раніше.
При перетині двох паралельних прямих третьою січною:
- внутрішні різносторонні кути рівні;
- відповідні кути рівні;
- сума односторонніх кутів дорівнює \(180°.\)