Дві прямі, що перетинаються під прямим кутом, називаються перпендикулярними.

Скорочено це записують так:
Відрізки або промені називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Теорема (про дві прямі, перпендикулярні до третьої).
Дві прямі, перпендикулярні до третьої, паралельні.
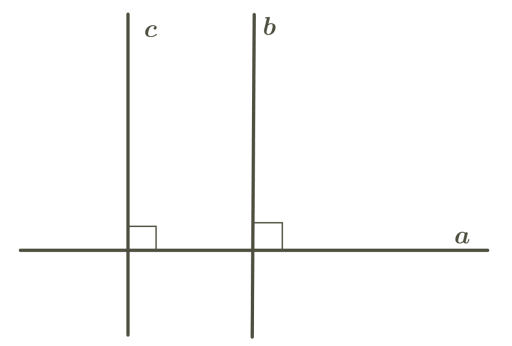
Твердження теореми ілюструє рисунок. На цьому рисунку
Ця властивість використовується для побудови паралельних прямих за допомогою лінійки та косинця. Двічі прикладаючи косинець до лінійки, можна провести дві прямі, перпендикулярні до краю лінійки.
Теорема (про існування і єдиність перпендикулярної прямої)
Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.
Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.
Зверни увагу!
Теорема містить два твердження:
\(1)\) існує пряма, що проходить через дану точку площини і є перпендикулярною до даної прямої;
\(2)\) така пряма єдина.
\(1)\) існує пряма, що проходить через дану точку площини і є перпендикулярною до даної прямої;
\(2)\) така пряма єдина.
Перпендикуляром до даної прямої, проведеним із точки A, називається відрізок прямої, перпендикулярної до даної, одним із кінців якого є точка А, а другим (основою перпендикуляра) — точка перетину цих прямих.
Відстанню від точки до прямої, яка не проходить через дану точку, називається довжина перпендикуляра, проведеного з даної точки до даної прямої.