Два кути, у яких одна сторона спільна, а дві інші сторони є доповняльними променями, називаються суміжними.
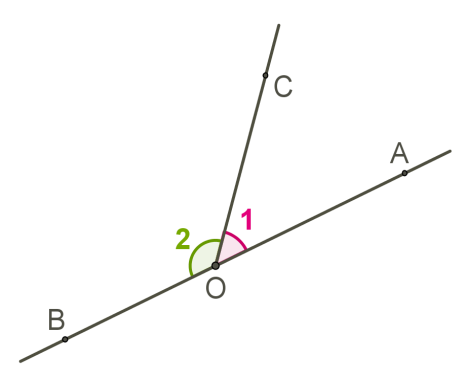
Оскільки — розгорнутий кут і промінь \(OC\) ділить його на дві частини, то\(.\)
Сума суміжних кутів дорівнює .
Зверни увагу!
Властивості суміжних кутів
- Якщо два кути рівні, то суміжні з ними кути також рівні.
- Два кути, суміжні з одним і тим самим кутом, рівні.
- Кут, суміжний і з прямим кутом, також прямий. Кут, суміжний із тупим кутом, гострий. Кут, суміжний із гострим кутом, тупий.
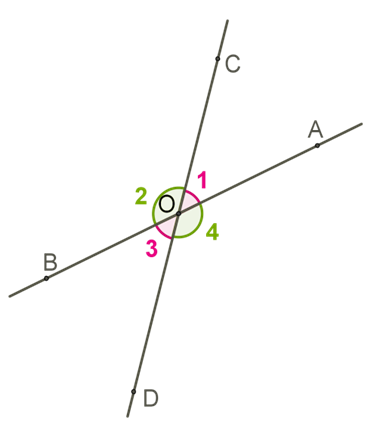
Якщо перетинаються дві прямі, то утворюються дві пари вертикальних кутів: і \(.\)
За властивістю суміжних кутів і \(.\) Отже,\(.\)
Також зрозуміло, що \(.\)
Вертикальні кути рівні.
Якщо один із вертикальних кутів прямий, тобто дорівнює \(,\) то інші кути також прямі.
Кутом між двома прямими, що перетинаються, називається менший із кутів, що утворилися в результаті перетину цих прямих.
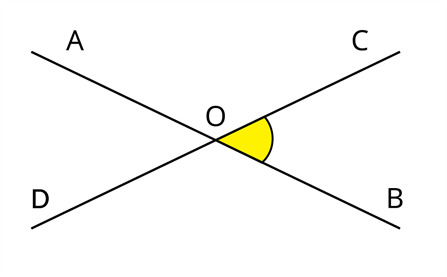
\(COB\) — кут між прямими \(CD\) і \(AB\).
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Прямі \(a\) і \(b\) перпендикулярні. Коротко це позначають так: \(.\)
Відрізки або промені називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Зверни увагу!
Властивість перпендикулярних прямих
Дві прямі, перпендикулярні до третьої, паралельні.
Дві прямі, перпендикулярні до третьої, паралельні.
Прямі \(a\) і \(b\) паралельні. Коротко це позначають так: \(.\)
Ця властивість використовується для побудови паралельних прямих за допомогою лінійки та косинця. Двічі прикладаючи косинець до лінійки, можна провести дві прямі, перпендикулярні до краю лінійки.
