Побудова трикутника за трьома елементами
Існують такі основні задачі на побудову за допомогою циркуля та лінійки:
\(1.\) Як провести коло з даними центром і радіусом.
\(2.\) Як на даному промені від його початку відкласти відрізок, рівний даному.
\(3.\) Як побудувати кут, рівний даному.
\(2.\) Як на даному промені від його початку відкласти відрізок, рівний даному.
\(3.\) Як побудувати кут, рівний даному.
\(4.\) Як провести бісектрису кута.
\(5.\) Як побудувати перпендикулярну пряму.
\(6.\) Як прокласти середину відрізка.
\(5.\) Як побудувати перпендикулярну пряму.
\(6.\) Як прокласти середину відрізка.
Використовуючи ці побудови й дані елементи трикутника, можна побудувати 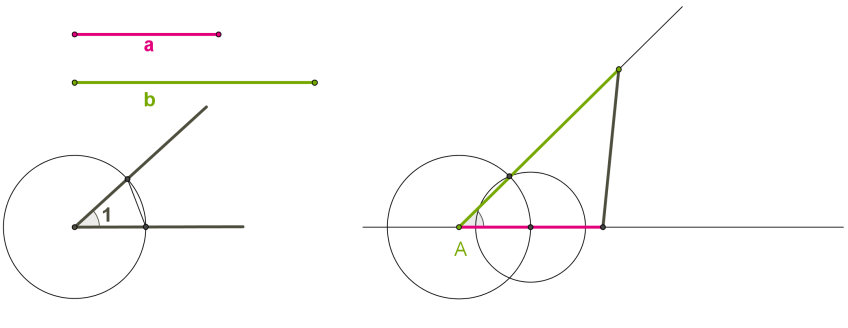
трикутник, рівний даному.
Приклад:
Побудова трикутника за двома сторонами й кутом між ними
Дано два відрізки \(a\) і \(b,\) які дорівнюють сторонам шуканого трикутника, і кут \(1,\) що дорівнює куту трикутника між сторонами. Необхідно побудувати трикутник із елементами, що дорівнюють даним відрізкам і куту.
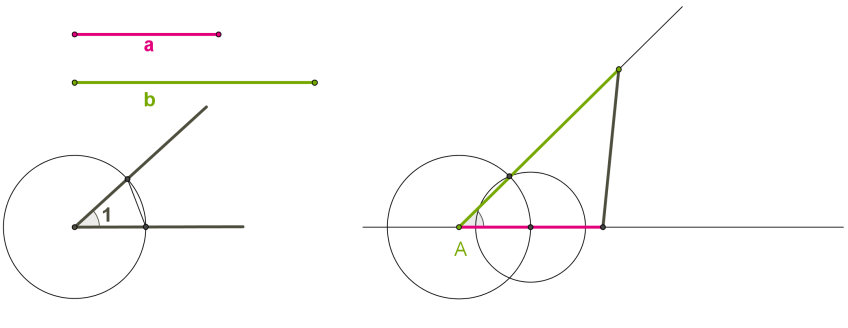
Кроки розв'язання
\(1.\) Провести пряму.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a.\)
\(3.\) Побудувати кут, що дорівнює даному \(1\) (вершина кута \(A,\) одна сторона кута лежить на прямій).
\(4.\) На іншій стороні кута відкласти відрізок, що дорівнює даному відрізку \(b.\)
\(5.\) З'єднати кінці відрізків.
Згідно з ознакою рівності трикутників за двома сторонами й кутом між ними, побудований трикутник дорівнює всім трикутникам, які мають дані елементи.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a.\)
\(3.\) Побудувати кут, що дорівнює даному \(1\) (вершина кута \(A,\) одна сторона кута лежить на прямій).
\(4.\) На іншій стороні кута відкласти відрізок, що дорівнює даному відрізку \(b.\)
\(5.\) З'єднати кінці відрізків.
Згідно з ознакою рівності трикутників за двома сторонами й кутом між ними, побудований трикутник дорівнює всім трикутникам, які мають дані елементи.
Побудова трикутника за стороною і двома прилеглими до неї кутами
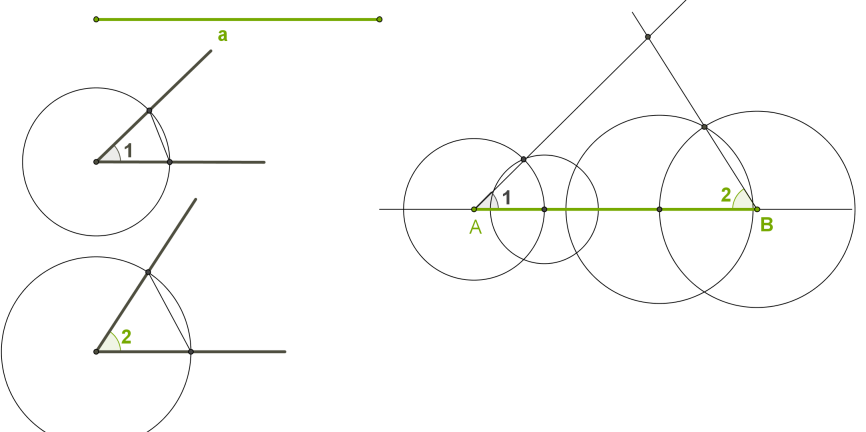
Дано відрізок \(a\) і два кути \(1\) і \(2,\) які дорівнюють кутам трикутника, прилеглим до даної сторони. Необхідно побудувати трикутник із елементами, які дорівнюють даному відрізку й кутам.

Кроки розв'язання
\(1.\) Провести пряму.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a,\) і позначити інший кінець відрізка \(B.\)
\(3.\) Побудувати кут, що дорівнює даному \(1\) (вершина кута \(A,\) одна сторона кута лежить на прямій).
\(4.\) Побудувати кут, що дорівнює даному \(2\) (вершина кута \(B,\) одна сторона кута лежить на прямій).
\(5.\) Точка перетину інших сторін кутів є третьою вершиною шуканого трикутника.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a,\) і позначити інший кінець відрізка \(B.\)
\(3.\) Побудувати кут, що дорівнює даному \(1\) (вершина кута \(A,\) одна сторона кута лежить на прямій).
\(4.\) Побудувати кут, що дорівнює даному \(2\) (вершина кута \(B,\) одна сторона кута лежить на прямій).
\(5.\) Точка перетину інших сторін кутів є третьою вершиною шуканого трикутника.
Згідно з ознакою рівності трикутників за стороною та двома прилеглими до неї кутами, побудований трикутник дорівнює усім трикутникам, які мають дані елементи.
Побудова трикутника за трьома сторонами
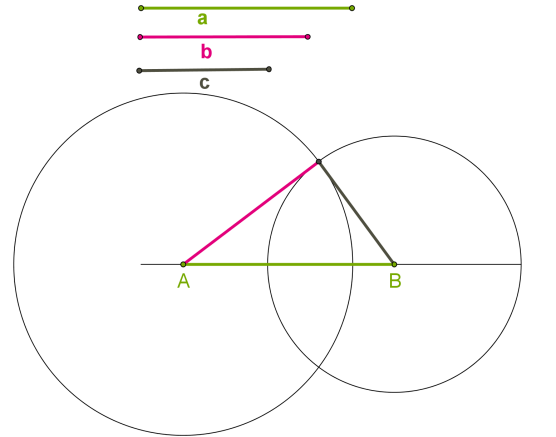
Дано три відрізки: \(a,\) \(b\) і \(c,\) що дорівнюють сторонам шуканого трикутника. Необхідно побудувати трикутник зі сторонами, що дорівнюють даним відрізкам.
Дано три відрізки: \(a,\) \(b\) і \(c,\) що дорівнюють сторонам шуканого трикутника. Необхідно побудувати трикутник зі сторонами, що дорівнюють даним відрізкам.
У цьому випадку перед початком побудови необхідно переконатися, чи виконується нерівність трикутника (довжина кожного відрізка менша від суми довжин двох інших відрізків), і ці відрізки можуть бути сторонами трикутника.

Якщо так, то виконати такі дії:
\(1.\) Провести пряму.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a,\) і позначити інший кінець відрізка \(B.\)
\(3.\) Провести коло з центром \(A\) і радіусом, що дорівнює відрізку \(b.\)
\(4.\) Провести коло з центром \(B\) і радіусом, що дорівнює відрізку \(c.\)
\(5.\) Точка перетину кіл є третьою вершиною шуканого трикутника.
\(2.\) На прямій від вибраної точки \(A\) відкласти відрізок, що дорівнює даному відрізку \(a,\) і позначити інший кінець відрізка \(B.\)
\(3.\) Провести коло з центром \(A\) і радіусом, що дорівнює відрізку \(b.\)
\(4.\) Провести коло з центром \(B\) і радіусом, що дорівнює відрізку \(c.\)
\(5.\) Точка перетину кіл є третьою вершиною шуканого трикутника.
Згідно з ознакою рівності трикутників за трьома сторонами, побудований трикутник дорівнює всім трикутникам, які мають дані сторони.
