Властивості прямокутного трикутника
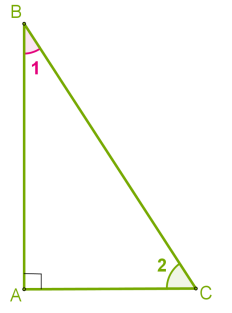
Прямокутний трикутник має один прямий і два гострі кути.
Сторона прямокутного трикутника, протилежна прямому куту, називається гіпотенузою, дві інші сторони — катетами.
На рисунку у трикутнику \(\triangle\)\(ABC:\)
\(\angle\)\(А = 90°,\) \(BC\) — гіпотенуза, \(AC\) \(і\) \(AB\) — катети.
З теореми про суму кутів трикутника випливає:
сума гострих кутів прямокутного трикутника дорівнює \(90°.\)
Справедливе також обернене твердження, що є ознакою прямокутного трикутника:
якщо в трикутнику сума двох кутів дорівнює \(90°,\) то цей трикутник прямокутний.
\(1 +\) \(2 =\) \(.\)
Ознаки рівності прямокутних трикутників
Користуючись ознаками рівності трикутників і теоремою про суму кутів трикутника, можна сформулювати ознаки рівності характерні тільки для прямокутних трикутників:
\(1.\) Ознака рівності прямокутних трикутників за двома катетами
Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного
трикутника, то такі трикутники рівні.
Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного
трикутника, то такі трикутники рівні.
\(2.\) Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом
Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету
й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету
й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.
\(3.\) Ознака рівності прямокутних трикутників за катетом і протилежним кутом
Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.
\(4.\) Ознака рівності прямокутних трикутників за гіпотенузою й гострим кутом
Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому
куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому
куту другого прямокутного трикутника, то такі трикутники рівні.
\(5.\) Ознака рівності прямокутних трикутників за гіпотенузою й катетом
Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого
прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого
прямокутного трикутника, то такі трикутники рівні.
Прямокутний трикутник із кутом \(30°\)
Катет прямокутного трикутника, що лежить навпроти кута \(,\) дорівнює половині гіпотенузи (гіпотенуза удвічі довша від катета навпроти кута ).
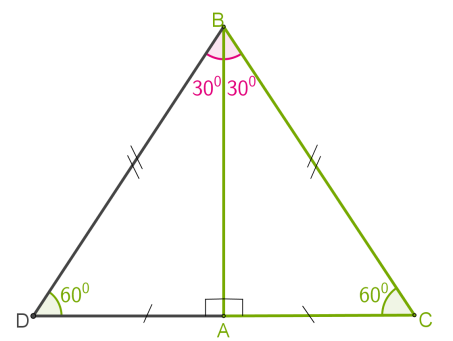
Розглянемо прямокутний трикутник \(ABC,\) у якому:
\(A\) — прямий, \(B =\) \(,\) отже \(C =\) \(.\)
Доведемо, що \(BC = 2 AC.\)
\(1.\) Прикладемо до трикутника \(\triangle\)\(ABC\) рівний йому трикутник \(\triangle\)\(ABD,\) як показано на рисунку. У них:
\( C =\) \(D =\) \(,\) як відповідні кути рівних трикутників.
\(AD = AC,\) як відповідні сторони рівних трикутників.
\(2.\) Отримаємо трикутник \(\triangle\)\(BCD,\) у якому:
\(C =\) \(D =\) \(,\) то \(B =\) \(,\) за теоремою про суму кутів трикутника.
\(3.\) Проти рівних кутів лежать рівні сторони. Звідси \(BC = DC = BD.\) Але \(DC = 2 AC.\) Отже, \(BC = DC = 2 AC.\)
Правильним є і обернене твердження:
Якщо катет прямокутного трикутника дорівнює половині гіпотенузи (або гіпотенуза удвічі довша від катета), то кут, що лежить навпроти цього катета, дорівнює \(.\)