Рівнобедрений трикутник
Трикутник, у якого всі сторони різні, називається різностороннім.
Трикутник називається рівнобедреним, якщо в нього дві сторони рівні.
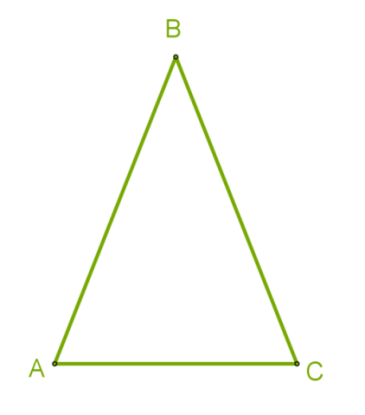
На рисунку зображено рівнобедрений трикутник \(ABC\) з бічними сторонами \(AB\) \(і\) \(BC\) та основою \(AC.\)
Трикутник називається рівностороннім, якщо в нього всі сторони рівні.
Зверни увагу!
Зазначимо, що рівносторонній трикутник також є рівнобедреним, причому будь-які дві його сторони можна вважати бічними.
Рівнобедрений трикутник має властивості, яких не мають різносторонні трикутники:
\(1.\) У рівнобедренному трикутнику кути, прилеглі до основи, є рівними.
\(2.\) У рівнобедренному трикутнику бісектриса, проведена до основи, є медіаною і висотою.
\(3.\) У рівнобедренному трикутнику медіана, проведена до основи, є бісектрисою і висотою.
\(4.\) У рівнобедренному трикутнику висота, проведена до основи, є бісектрисою і медіаною.
Першу й другу властивості можна довести, якщо доведемо рівність двох трикутників, які утворюються, коли з протилежного до основи кута провести бісектрису \(BD.\)
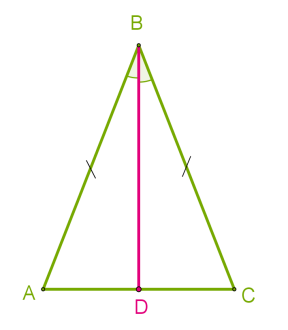
Розглянемо рівнобедрений трикутник \(ABC\) з основою \(AC\) і доведемо, що \(.\)
Нехай \(BD\) — бісектриса трикутника \(ABC.\)
за першою ознакою рівності трикутників.
\(1.\) \(AB = BC,\) як бічні сторони рівнобедреного трикутника.
\(2.\) \(BD\) — спільна сторона.
\(3.\) \(,\) за властивістю бісектриси.
У рівних трикутників відповідні сторони і відповідні кути рівні:
\(1.\) — доведено, що прилеглі до основи кути рівні.
\(2.\) \(AD = DC\) — доведено, що бісектриса є медіаною.
\(3.\) — оскільки суміжні кути, сума яких дорівнює \(,\) рівні, то кожен із них дорівнює \(,\) тобто медіана є висотою.
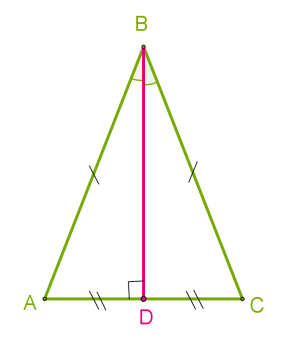
Третю і четверту властивості можна легко довести самостійно.
Наслідок
У рівносторонньому трикутнику всі кути рівні.
У рівносторонньому трикутнику всі кути рівні.
Ознака рівнобедреного трикутника
Якщо в трикутнику два кути рівні, то він рівнобедрений.
Якщо в трикутнику два кути рівні, то він рівнобедрений.
Наслідок (ознака рівностороннього трикутника)
Якщо в трикутнику всі кути рівні, то він рівносторонній.
Якщо в трикутнику всі кути рівні, то він рівносторонній.
Наслідок
У рівносторонньому трикутнику медіана, бісектриса й висота, проведені з однієї вершини, збігаються.
У рівносторонньому трикутнику медіана, бісектриса й висота, проведені з однієї вершини, збігаються.
Зверни увагу!
На практиці для розв’язування задач замість доведеної теореми часто використовують твердження про збіг лише двох із трьох зазначених відрізків:
\(1)\) якщо в трикутнику медіана й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним;
\(2)\) якщо в трикутнику бісектриса й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним;
\(3)\) якщо в трикутнику медіана й бісектриса, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним.
\(1)\) якщо в трикутнику медіана й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним;
\(2)\) якщо в трикутнику бісектриса й висота, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним;
\(3)\) якщо в трикутнику медіана й бісектриса, проведені з однієї вершини, збігаються, то такий трикутник є рівнобедреним.