У трикутнику навпроти більшої сторони лежить більший кут.
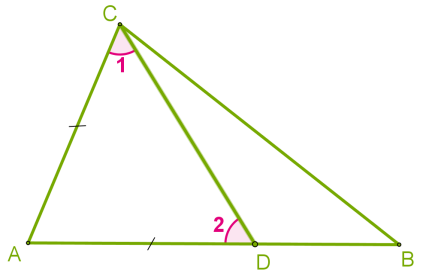
Доведення
Нехай у трикутнику \(ABC\) сторона \(AB\) більша від сторони \(AC.\)
Доведемо, що \(C >\) \(B.\)
\(1.\) Відкладемо на стороні \(AB\) відрізок, рівний стороні \(AC.\)
\(\triangle\)\(CAD\) — рівнобедрений.
\(2.\) Оскільки \(AD <AB,\) то точка \(D\) лежить між точками \(A\) і \(B.\)
Отже, кут \(1\) є частиною кута \(C\) і, відповідно:
\(C >\) \(1\)
\(3.\) Кут \(2\) — зовнішній кут трикутника \(BDC,\) тому \(2 >\) \(B.\)
\(1 =\) \(2\) (оскільки це кути при основі рівнобедреного трикутника \(ADC\))
Отже, \(C >\) \(1 =\) \(2 >\) \(B.\)
Звідси випливає, що \(C >\) \(B.\)
Правильною є і обернена теорема.
У трикутнику навпроти більшого кута лежить більша сторона.
Висновок 1. Якщо два кути трикутника рівні, то трикутник рівнобедрений (ознака рівнобедреного трикутника).
Висновок 2. Якщо три кути трикутника рівні, то трикутник рівносторонній.
Висновок 3. У прямокутному трикутнику гіпотенуза більша від катета.
Висновок 4. У тупокутному трикутнику сторона, яка лежить проти тупого кута, найбільша.
Нерівність трикутника
Кожна сторона трикутника менша, ніж сума двох інших сторін.
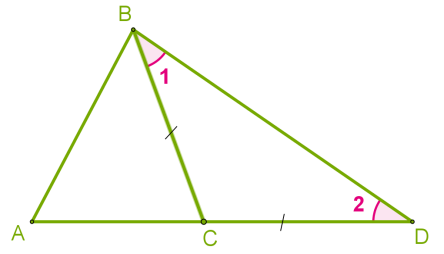
Доведення
Розглянемо трикутник\(ABC\) і доведемо, що \(AB < AC + BC.\)
Продовжимо сторону \(AC\) й відкладемо відрізок \(CD = BC.\)
Трикутник \(BCD\) — рівнобедрений, отже \(1 = \) \(2.\)
У трикутнику \(ABD\) очевидно, що \(ABD >\) \(1,\) що означає: \(ABD >\) \(2.\)
Оскільки навпроти більшого кута лежить більша сторона, \(AB < AD,\) а \(AD\) \(=\)
\(AB < AC + CB, AC < AB + BC, BC < AB + AC\)
\(AC\) \(+\) \(BC,\) отже:
\(AB < AC + BC\)
Висновок 5. Для будь-якої з трьох точок \(A, B\) і \(C,\) що не лежать на одній прямій, правильними є нерівності:
\(AB < AC + CB, AC < AB + BC, BC < AB + AC\)
Висновок 6. Якщо для трьох точок \(A, B, C\) справджується рівність \(АС = АВ + ВС,\) то ці точки лежать на одній прямій, причому точка \(B\) лежить між точками \(A\) \(і\) \(C.\)
Нерівність трикутника дозволяє проаналізувати існування, а отже, і можливість побудови трикутника із заданими сторонами. Зокрема, якщо хоч одне з трьох додатних чисел \(a, b, c\) більше за суму двох інших або дорівнює їй, то побудувати трикутник зі сторонами \(a, b, c\) неможливо.