Сума кутів трикутника
Сума кутів трикутника дорівнює \(180°.\)
Доведення
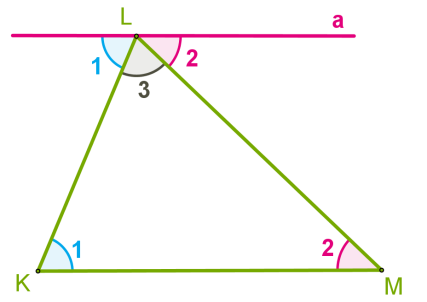
Розглянемо довільний трикутник \(KLM\) і доведемо, що
\(K +\) \(L\) \(+\) \(M =\)
\(1.\) Проведемо через вершину \(L\) пряму \(a,\) паралельну стороні \(KM.\)
\(2.\) Кути, позначені цифрою \(1,\) є внутрішніми різносторонніми кутами при перетині паралельних прямих \(a\) і \(KM\) січною \(KL.\)
\(3.\) Кути, позначені цифрою \(2,\) — внутрішніми різносторонніми кутами при перетині тих самих паралельних прямих січною \(ML.\)
\(4.\) Очевидно, що сума кутів \(1,\) \(2\) і \(3\) дорівнює розгорнутому куту з вершиною \(L,\) тобто:
\(1 +\) \(2\) \(+\) \(3 =\)
або
\(K +\) \(L\) \(+\) \(M =\)
Теорему доведено.
Зверни увагу!
Висновки з теореми про суму кутів трикутника
Висновок 1. Сума гострих кутів прямокутного трикутника дорівнює \(.\)
Висновок 2. У рівнобедреному прямокутному трикутнику кожен гострий кут дорівнює \(.\)
Висновок 3. У будь-якому трикутнику або всі кути гострі, або два кути гострі, а третій тупий або прямий.
Зовнішній кут трикутника
Зовнішнім кутом трикутника називається кут, суміжний із внутрішнім кутом даного трикутника.
Теорема (про зовнішній кут трикутника)
Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.
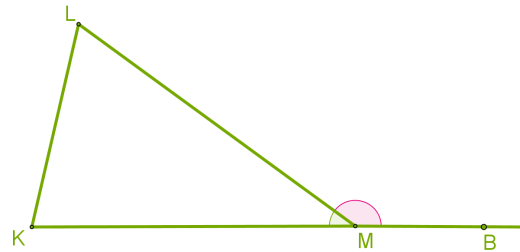
Доведення
Із рівностей
\(KML\) \(+\) \(BML\) \(=\)
і
\(K +\) \(L\) \(+\) \(KML =\)
отримуємо, що:
\(BML =\) \(K\) \(+\) \(L\)
Наслідок
Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.
Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.
Гострокутний, прямокутний і тупокутний трикутники
Як свідчить четвертий висновок із теореми про суму кутів трикутника, можна виокремити три види трикутників залежно від кутів.
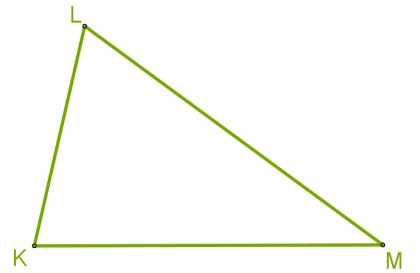
У трикутника \(KLM\) усі кути гострі.
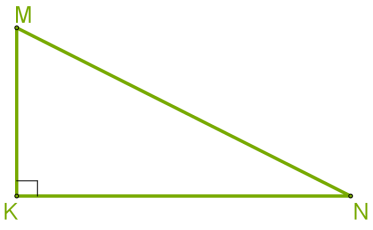
У трикутника \(KLM\) кут \(K = 90\)\(.\)
У прямокутного трикутника сторона, що лежить навпроти прямого кута, називається гіпотенузою, а дві інші сторони — катетами.
На рисунку \(MN\) — гіпотенуза, \(KN\) і \(KM\) — катети.
У трикутника \(KLM\) один кут тупий.