Третя ознака рівності трикутників
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.
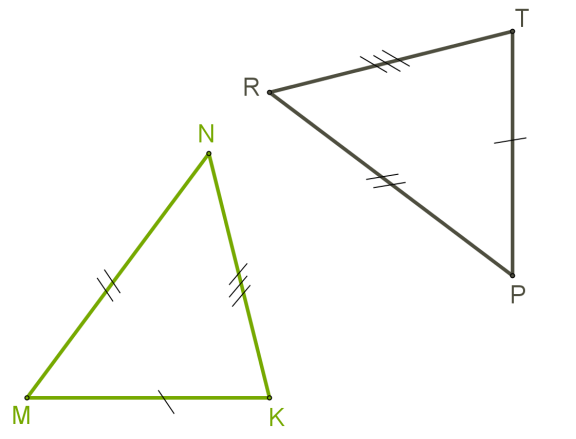
Спробуємо поєднати трикутники і за допомогою накладання й переконатися, що відповідна рівність сторін гарантує рівність відповідних кутів цих трикутників, і вони повністю збігаються.
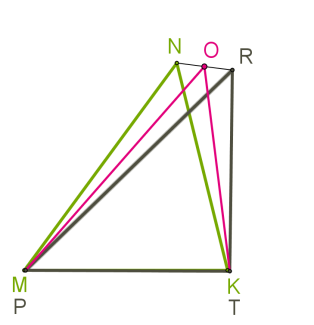
\(1.\) Сумістимо, наприклад, однакові відрізки \(MK\) і \(PT.\) Припустимо, що точки \(N\) і \(R\) при цьому не суміщаються.
\(2.\) Нехай \(O\) — середина відрізка \(NR.\) Відповідно до цієї інформації, \(,\) \(.\)
\(3.\) Трикутники \(MNR\) і \(KNR\) — рівнобедрені зі спільною основою \(NR.\) Тому їх медіани \(MO\) і \(KO\) є висотами, отже, вони перпендикулярні до \(NR.\)
\(4.\) Прямі \(MO\) і \(KO\) не суміщаються. Точки \(M,\) \(K,\) і \(O\) не лежать на одній прямій. Але через точку \(O\) до прямої \(NR\) можна провести лише одну перпендикулярну їй пряму.
Ми отримали суперечність. Отже, доведено, що повинні поєднатися й вершини \(N\) і \(R.\)
Третя ознака дозволяє назвати трикутник дуже сильною, стійкою фігурою. Іноді говорять, що трикутник — жорстка фігура. Якщо довжини сторін не змінюються, то кути також не змінюються.
Третя ознака дозволяє назвати трикутник дуже сильною, стійкою фігурою. Іноді говорять, що трикутник — жорстка фігура. Якщо довжини сторін не змінюються, то кути також не змінюються.
Наприклад, у чотирикутника такої властивості немає. Саме тому різні підмоги й кріплення роблять трикутними.



Своєрідну стійкість, стабільність і досконалість числа \(3\) люди оцінювали й виокремлювали з давніх-давен.
Про це свідчать казки, у яких є «три ведмеді», «три вітри», «троє поросят», «троє товаришів», «три брати», «три щасливці», «троє умільців», «троє друзів», «три богатирі» і т. ін.
Також там ідеться про «три спроби», «три поради», «три вказівки», «три зустрічі», виконуються «три бажання», потрібно потерпіти «три дні», «три ночі», «три роки», пройти через «три держави», «три підземних царства», витримати «три випробування», перепливти через «три моря» тощо.

І на закінчення ще раз пригадаємо всі ознаки рівності трикутників:
\(1.\) Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.
\(2.\) Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.
\(3.\) Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.
\(2.\) Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.
\(3.\) Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.