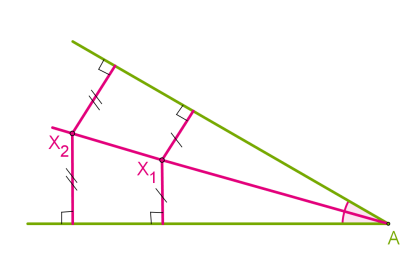
Теорема 1. Кожна точка бісектриси нерозгорнутого кута рівновіддалена від його сторін.
Теорема 2 (протилежна). Точка, що лежить усередині нерозгорнутого кута й рівновіддалена від його сторін, лежить на бісектрисі цього кута.
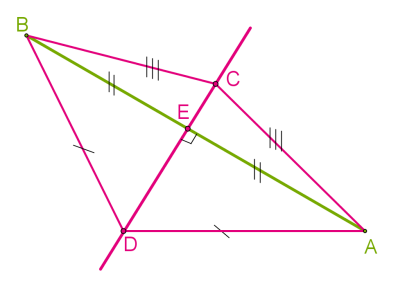
Теорема 3. Кожна точка серединного перпендикуляра до відрізка рівновіддалена від його кінців.
Теорема 4 (протилежна). Точка, рівновіддалена від кінців відрізка, лежить на серединному перпендикулярі до нього.
Перша визначна точка трикутника — точка перетину бісектрис.
Теорема 5. Бісектриси трикутника перетинаються в одній точці.
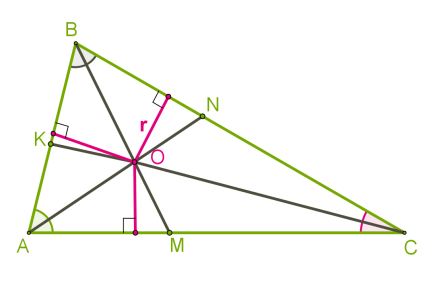
\(AN,\) \(BM\) — бісектриси, \(O\) — точка їх перетину.
Чи є бісектрисою \(CK\)\(?\) Якщо точка \(O\) рівновіддалена від сторін \(AB\) і \(AC\) та від сторін \(BA\) і \(BC,\) то вона лежить на бісектрисі \(,\) оскільки рівновіддалена від сторін кута.
Ця точка і є центром кола, вписаного в трикутник. Вона завжди розташовується в трикутнику.
Друга визначна точка трикутника — точка перетину серединних перпендикулярів сторін трикутника.
Теорема 6. Серединні перпендикуляри до сторін трикутника перетинаються в одній точці.
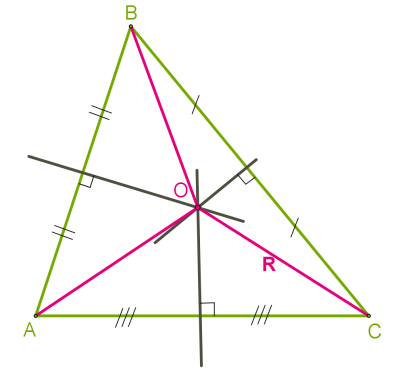
Припустимо, точка \(O\) — точка перетину двох серединних перпендикулярів сторін \(AB\) і \(BC.\) Вона рівновіддалена від точок \(A\) і \(B,\) і від точок \(B\) і \(C.\) Отже, вона лежить на серединному перпендикулярі сторони \(AC,\) оскільки рівновіддалена від її кінцевих точок.
Ця точка і є центром кола, описаного навколо трикутника. Вона розташовується в трикутниках із гострими кутами, поза трикутником із тупим кутом і на гіпотенузі прямокутного трикутника.
Третя визначна точка трикутника — точка перетину медіан.
Теорема 7. Медіани трикутника перетинаються в одній точці, яка ділить кожну медіану у співвідношені \(2\) \(:\) \(1,\) рахуючи від вершини.
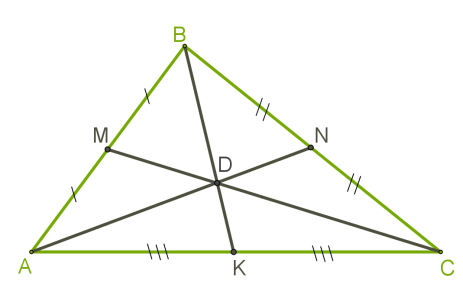
Точка перетину медіан є центром ваги трикутника.
Четверта визначна точка трикутника — точка перетину висот трикутника
Теорема 8. Висоти трикутника або їхні продовження перетинаються в одній точці.
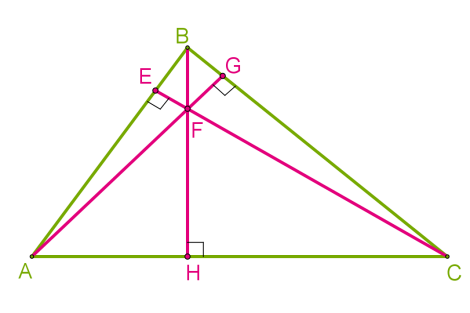
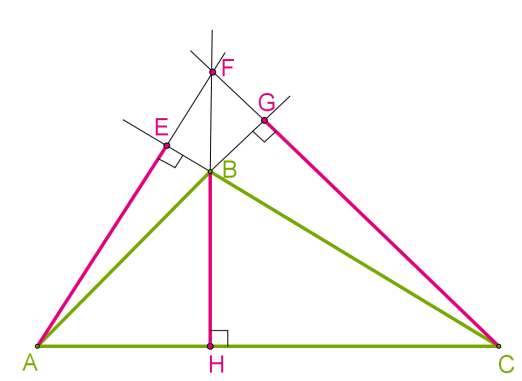
Точка перетину висот називається ортоцентром трикутника.
У \(1765\) році німецький математик Ейлер довів, що в будь-якому трикутнику ортоцентр, центр ваги і центр описаного кола лежать на одній прямій, яку назвали прямою Ейлера.
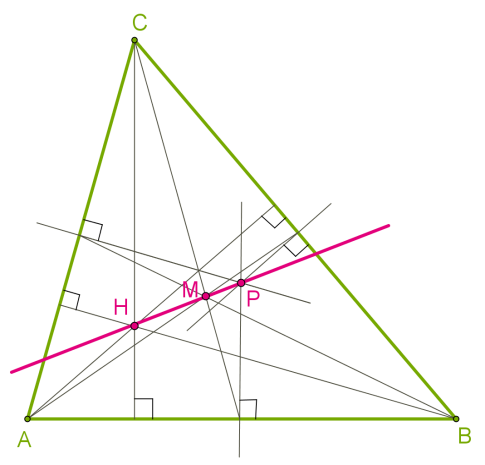
У \(20\) \(рр.\) \(XIX\) \(ст.\) французькі математики Понселе, Бріаншона та інші встановили (незалежно один від одного) наступну теорему:
Основи медіан, основи висот і середини відрізків висот, що з'єднують ортоцентр із вершинами трикутника, лежать одному й тому самому колі.
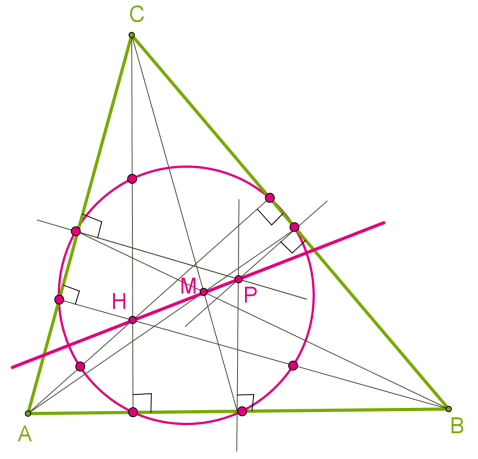
Точка перетину бісектрис — інцентр.
Точка перетину серединних перпендикулярів — центр описаного кола.
Точка перетину медіан — центроїд (центр мас).
Точка перетину висот — ортоцентр.
