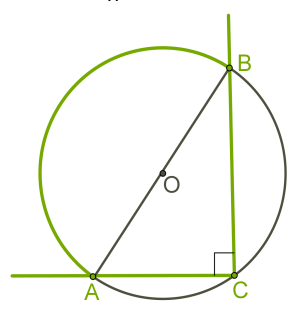
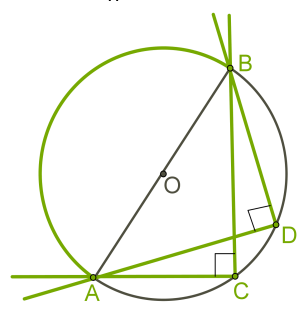
Якщо на колі позначити дві точки, вони поділять коло на дві дуги.
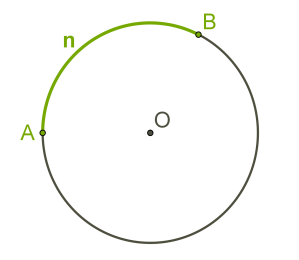
Є декілька способів того, як розрізняти за назвою, яку з дуг маємо на увазі. Один із них — використовувати в назві маленькі букви латинського алфавіту: \(.\)
Також можна поставити додаткову точку і в назві, а як третю букву використовувати назву точки — велику букву латинського алфавіту.
У кожної дуги є градусна міра.
Сума градусних мір двох дуг зі спільними кінцями дорівнює \(.\)
Якщо відрізок, що з'єднує кінці дуги, є діаметром кола, то дугу називають півколом.
Градусна міра півкола дорівнює \(.\)
Центральний і вписаний кути
Кут із вершиною в центрі кола називається центральним кутом.
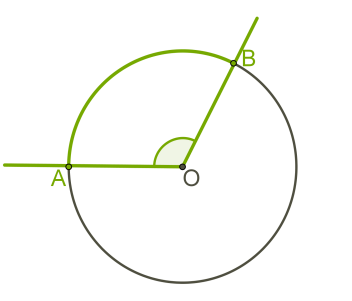
Градусна міра центрального кута дорівнює градусній мірі відповідної дуги кола:
\(AOB =\) \(AB\)
Кут, вершина якого лежить на колі, а сторони перетинають коло, називається вписаним кутом.
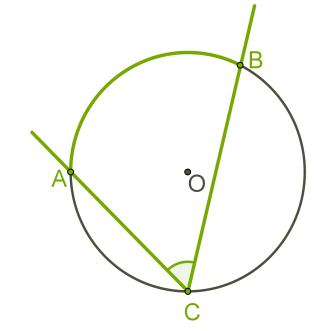
Вписаний кут вимірюється половиною дуги, на яку він спирається:
\(1.\) Вписані кути, що спираються на одну й ту саму дугу, рівні.
\(2.\) Вписаний кут, що спирається на півколо, дорівнює \(.\)
\(2.\) Вписаний кут, що спирається на півколо, дорівнює \(.\)