Площа паралелограма, трикутника і трапеції

www.ua.pistacja.tv

Площа паралелограма

Необхідно визначити, що таке висота паралелограма.

Це перпендикуляр, проведений з будь-якої точки сторони паралелограма до прямої, що містить протилежну паралельну сторону. Зазвичай, висоту проводять з вершини паралелограма. Оскільки паралелограм має дві пари паралельні сторони, тоді він має висоти двох різних довжин.

Висота \(BE\), проведена між довгими сторонами, коротше висоти \(BF\), проведеної між короткими сторонами.

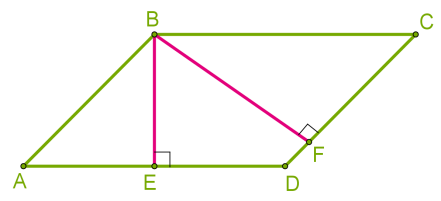
Оскільки сторони ромба однакові, тоді висоти ромба також однакові \(BE = BF\).

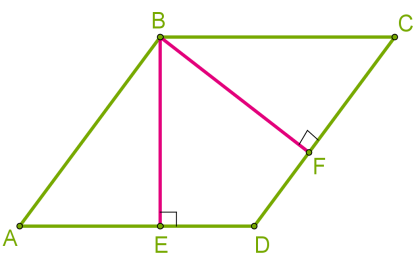
Площа довільного паралелограма

Площа паралелограма дорівнює добутку висоти і сторони, до якої проведена висота.

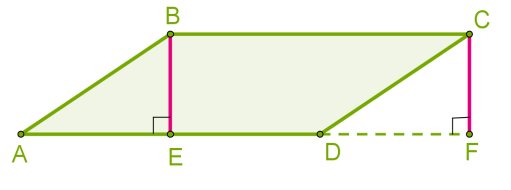
Проведемо висоти з двох вершин \(B\) і \(C\) до сторони \(AD\) .

Прямокутні трикутники \(ABE\) і \(DCF\) рівні (рівні гіпотенузи, як протилежні сторони паралелограма і рівні катети, як відстань між паралельними прямими).

Паралелограм \(ABCD\) і прямокутник \(EBCF\) — рівновеликі, оскільки складаються з рівних фігур:

\begin{array}{l} S_{ABCD} = S_{ABE} + S_{EBCD} \\ S_{EBCF} = S_{EBCD} + S_{DCF} \end{array}

Отже, площа паралелограма визначається так само, як площа прямокутника:

\begin{array}{l} S_{EBCF} = BE \cdot BC \\ S_{ABCD} = BE \cdot BC = BC \cdot AD \end{array}

Якщо позначити сторону через \(a\), висоту через \(h\), тоді:

S_{п - гр} = a \cdot h

Для визначення площі паралелограма можна використовувати коротку сторону і висоту, проведену до короткої сторони.

Площа ромба

Діагоналі ромба в точці перетину діляться навпіл, вони перпендикулярні і ділять ромб на чотири рівних прямокутних трикутника.

S_{ABCD} = 4 \cdot S_{ABO} = 4 \cdot \frac{BO \cdot AO}{2} = 2 \cdot BO \cdot AO

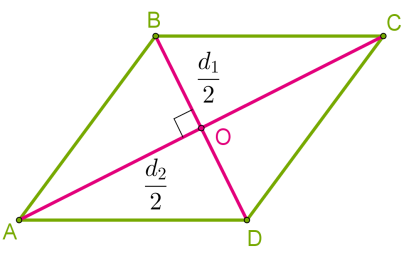
Формула визначення площі ромба:

S_{ромба} = \frac{d_{1} \cdot d_{2}}{2}

Ця формула справедлива для визначення площі будь-якого чотирикутника, якщо його діагоналі перпендикулярні.

Оскільки діагоналі квадрата рівні, тоді для визначення площі квадрата у формулі достатньо довжини однієї діагоналі:

S_{квадрата} = \frac{d^{2}}{2}

Площа довільного трикутника

Оскільки діагональ паралелограма ділить його на два рівних трикутника, тоді площа трикутника дорівнює половині площі паралелограма.

S_{трик} = \frac{a h_{a}}{2}

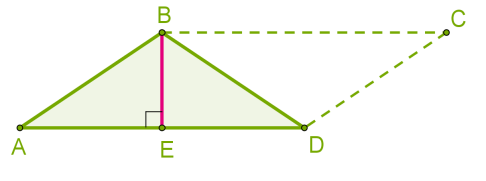
, де \(h\) — висота (на малюнку — \(BE\)), проведена до сторони \(a\) (на малюнку — \(AD\)).

Для визначення площі трикутника можна використовувати будь-яку сторону і висоту, проведену до цієї сторони.

Зручно іноді використовувати формулу Герона, якщо відомі довжини всіх трьох сторін трикутника.

\begin{array}{l} S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)} \\ p = \frac{a + b + c}{2} \end{array}

— формула Герона, де \(a, b\) і \(c\) — сторони трикутника, \(p\) — півпериметр трикутника.

Площа прямокутного трикутника

Оскільки катети прямокутного трикутника взаємно перпендикулярні, тоді один катет може бути висотою, а інший катет — стороною, до якої проведена висота. Отримуємо формулу:

S = \frac{a \cdot b}{2}

, де \(a\) і \(b\) — катети.

Для прямокутного трикутника можна застосовувати формули площі довільного трикутника.

Приклад:

1. Обчислимо площу трикутника зі сторонами \(17\) см, \(39\) см, \(44\) см.

Розв'язання:

\begin{array}{l} p = \frac{17 + 39 + 44}{2} = 50 \\ S_{Δ} = \sqrt{50 \cdot (50 - 17) \cdot (50 - 39) \cdot (50 - 44)} = \sqrt{50 \cdot 33 \cdot 11 \cdot 6} = \\ = \sqrt{25 \cdot 2 \cdot 3 \cdot 11 \cdot 11 \cdot 2 \cdot 3} = 5 \cdot 2 \cdot 3 \cdot 11 = 330 ({см}^{2}) \end{array}

Щоб легше було вирахувати корінь, необхідно розкладати числа на множники:

\sqrt{a \cdot a} = a

Формулу Герона можна використовувати для обчислення висоти трикутника.

Приклад:

2. Обчислимо меншу висоту трикутника, сторони якого дорівнюють \(15\) см, \(13\) см, \(4\) см.

Розв'язання:

Використовуємо дві формули обчислення площі:

S_{Δ} = \frac{a h_{a}}{2}

S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)}

Менша висота у трикутнику та, яка проведена до більшої сторони, тому \(a =\) \(15\) см.

S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{16 \cdot 1 \cdot 3 \cdot 12} = 24 ({см}^{2})

Утворюємо рівняння:

\begin{array}{l} \frac{15 \cdot h}{2} = 24| \cdot 2 \\ 15 \cdot h = 48 \\ h = \frac{48}{15} = 3,2 (см) \end{array}

Іноді формула Герона використовується для обчислення площі паралелограма, якщо дано сторони паралелограма і його діагональ.

Приклад:

3. Дано паралелограм зі сторонами \(17\) см і \(39\) см, довжина діагоналі дорівнює \(44\) см. Обчислимо площу паралелограма.

Розв'язання:

Діагональ ділить паралелограм на два рівних трикутника. Використовуємо результат, отриманий у першому прикладі:

S_{паралелограма} = 2 \cdot S_{Δ} = 2 \cdot 330 = 660 ({см}^{2})

Площа трапеції

Трапеція має одну пару паралельних сторін, отже, має одну висоту — перпендикуляр, проведений між паралельними сторонами.

Найчастіше висоту трапеції проводять з вершин або через точку перетину діагоналей.

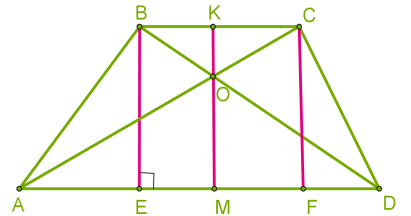
Площу трапеції визначимо, як суму площ трикутників, на які трапецію ділить діагональ.

\begin{array}{l} S_{ABCD} = S_{ABD} + S_{DBC} \\ S_{ABCD} = \frac{AD \cdot BE}{2} + \frac{BC \cdot DF}{2} = \frac{AD \cdot BE}{2} + \frac{BC \cdot BE}{2} = \\ = \frac{(AD + BC) \cdot BE}{2} \end{array}

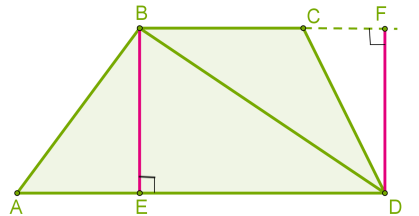
Якщо позначити паралельні сторони (основи) трапеції через \(a\) і \(b\), висоту через \(h\), тоді:

S_{трап} = \frac{a + b}{2} \cdot h

Зверни увагу!

1. Якщо висоти трикутників рівні, тоді їх площі відносяться, як довжини основ.

2. Якщо основи трикутників рівні, тоді їх площі відносяться, як довжини висот.

3. Якщо висоти трикутників рівні і їх основи рівні, тоді вони рівновеликі, наприклад, медіана ділить трикутник на дві рівновеликі частини.

Попередня тема

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!

1. Площа паралелограма, трикутника і трапеції

Теорія: