Подібність
Подібними фігурами можуть бути не тільки трикутники. Якщо змінити (збільшити або зменшити) всі розміри будь-якої плоскої фігури в одне і те ж число разів (відношення подібності), тоді стара і нова фігури називаються подібними за умови, що в двох подібних фігурах будь-які відповідні кути рівні.
Також два тіла можуть бути подібні, якщо одне з них може бути отримане з іншого шляхом збільшення (або зменшення) всіх його лінійних розмірів в одному і тому ж відношенні.
Наприклад, картина і її фотографія — це подібні фігури. Карти однієї і тієї ж території, зроблені в різних маштабах, подібні.
Автомобіль і його модель — подібні тіла, також будь-який макет подібний оригіналу, якщо його зроблено дотримуючись маштабу до всіх розмірів.
З геометричних фігур завжди подібні:
всі квадрати,
всі рівносторонні трикутники,
всі кола,
всі окружності.
всі квадрати,
всі рівносторонні трикутники,
всі кола,
всі окружності.
У завданнях шкільного курсу геометрії все-таки частіше будуть використані подібні трикутники. Далі розглянемо, як у різних ситуаціях утворюються подібні трикутники, або, як їх використовувати для розв'язання проблем.
Середня лінія трикутника
Відрізок, що сполучає середини двох сторін трикутника, називається середньою лінією цього трикутника.
Середня лінія трикутника паралельна одній з його сторін і дорівнює половині цієї сторони.
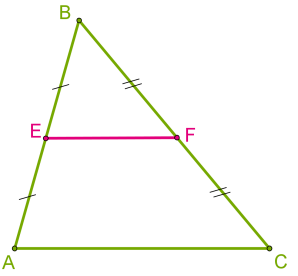
У кожному трикутнику три середніх лінії.
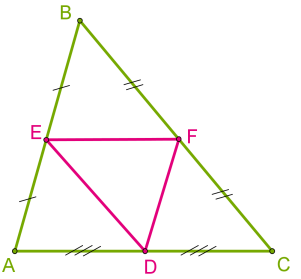
Середні лінії \(DE\), \(EF\), \(DF\).
Зверни увагу!
Даний трикутник \(ABC\) і трикутник \(FDE\), утворений середніми лініями, подібні за ознакою подібності за трьома пропорційними сторонами.
Пропорційні відрізки в прямокутному трикутнику
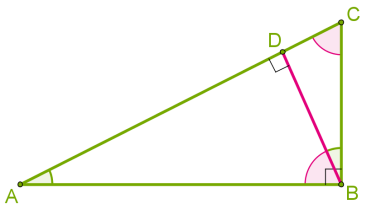
Якщо в прямокутному трикутнику провести висоту до гіпотенузи, отримуємо три пари прямокутних трикутників за ознакою подібності про рівні кути, оскільки і , отже, .
Практичні додатки подібності трикутників
1. Визначення висоти важко вимірюваного предмета.
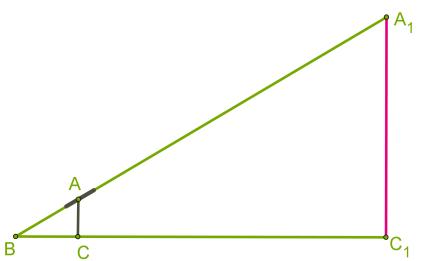
За допомогою жердини \(AC\) з планкою, що обертається, яка направляється до верхньої недоступної точки , розглядаються подібні трикутники \(ABC\) і .
2. Визначення відстані до недоступної точки.
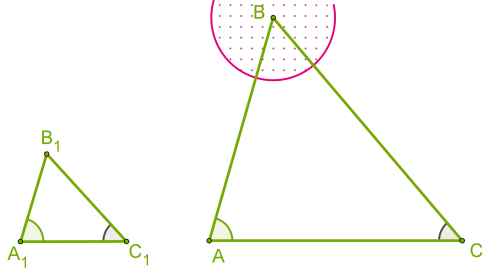
Вимірюється відрізок \(AC\), за допомогою необхідних інструментів вимірюються кути \(A\) і \(C\), будується подібний трикутник , в якому проводяться подальші вимірювання.
