У прямокутному трикутнику тригонометричні функції використовуються для обчислення сторін і гострих кутів трикутника.
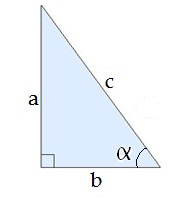
Як обрати правильну функцію?
Якщо використовуються тільки катети, застосовується tg.
Якщо використовується гіпотенуза (дано або треба обчислити), тоді застосовуються sin або cos.
Якщо використовується протилежлий катет (дано або треба обчислити), тоді застосовується sin.
Якщо використовується прилеглий катет, тоді застосовується cos.
Якщо в трикутнику дано обидва гострих кута, краще на малюнку відзначити тільки один кут, щоб однозначно зрозуміти, де прилеглий і де протилежлий катет.
Гіпотенуза завжди в знаменнику.
Значення тригонометричних функцій (які потрібно знати напам'ять)
|
|
\(30\) | \(45\) |
\(60\)
|
| \(sin\)\(\) | |||
| \(cos\) | |||
| \(tg\)\(\) | \(1\ \) |
Величини інших кутів можна знайти в таблиці або обчислити за допомогою калькулятора.
Приклад:
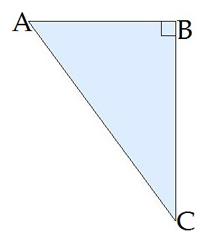
Дано: \(AB =\) \(6\) \(см\),
Обчислити: \(AC\)
Шуканий відрізок гіпотенуза, дано кут і прилеглий катет, тому будемо використовувати \(cos\).
Використання властивості прямокутного трикутника:
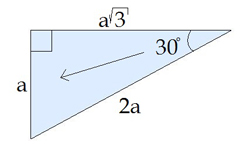
Катет прямокутного трикутника, що лежить навпроти кута в \(30\), дорівнює половині гіпотенузи.
Катет, який лежить навпроти кута в \(60\), дорівнює добутку меншого катета на .
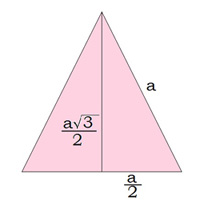
Дане співвідношення зручно використовувати для знаходження висоти рівностороннього трикутника.
Кут рівностороннього трикутника дорівнює \(60\), і бісектриса ділить цей кут навпіл.
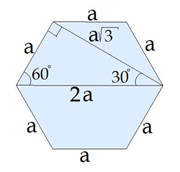
У правильному шестикутнику більша діагональ, менша діагональ і сторона шестикутника утворюють прямокутний трикутник, один з кутів якого дорівнює \(30\).