Коло, описане навколо трикутника
Коло називається описаним навколо трикутника, якщо всі вершини трикутника розташовані на колі.
Його центр рівновіддалений від усіх вершин, тобто повинен розміщуватися в точці перетину серединних перпендикулярів до сторін трикутника.
Отже, навколо будь-якого трикутника можна описати коло, оскільки серединні перпендикуляри до сторін перетинаються в одній точці.
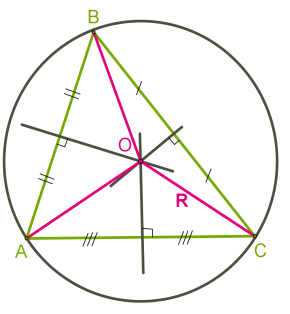
Для гострокутного трикутника центр кола розташований у трикутнику.
Інша ситуація з прямокутним і тупокутним трикутниками.
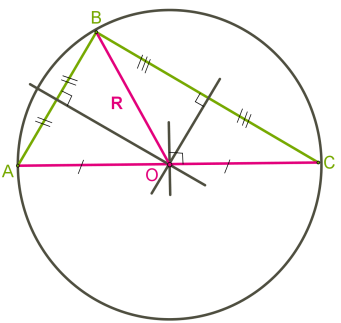
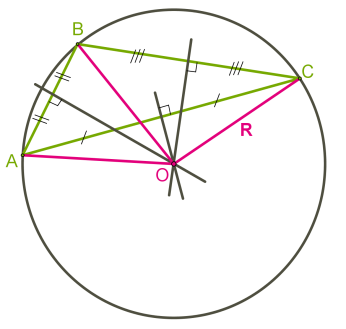
Коло, вписане в трикутник
Коло називається вписаним у трикутник, якщо всі сторони трикутника дотикаються до кола.
Отже, в будь-який трикутник можна вписати коло, оскільки бісектриси трикутника перетинаються в одній точці.
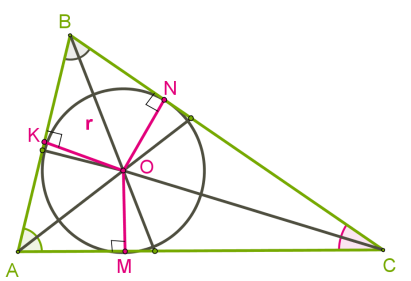
Оскільки бісектриси кутів трикутника завжди перетинаються всередині трикутника, то для всіх трикутників центр вписаного кола розташовується в трикутниках.
Формули (рівносторонній трикутник)
Зверни увагу!
У рівностороннього трикутника збігаються бісектриси, медіани й висоти, тобто ці відрізки є також серединними перпендикулярами. Це означає, що центри вписаного та описаного кіл збігаються.
Радіус описаного кола
\(,\) тому \(.\)
Радіус вписаного кола
\(,\) де \(h\) — висота трикутника.
Якщо дано сторону трикутника \(a,\) тоді \(.\)
Отже, \(.\)
Формули (прямокутний трикутник)
Радіус описаного кола
\(,\) де \(c\) — гіпотенуза.
Радіус вписаного кола
\(,\) де \(p\) — півпериметр.
Формули (довільний трикутник)
Радіус описаного кола
\(,\) де — кут, протилежний стороні \(a.\)
Радіус вписаного кола
\(,\) де \(p\) — півпериметр.
